Introduction to Stack Data Structure.

Created On: 28 December 2023

What is a Stack?

A stack is a linear data structure that operates on the principle of Last In, First Out (LIFO). This means that the last element added to the stack is the first one to be removed.


Imagine a stack of books. When you add a new book, it goes on top of the pile. To access the books, you start from the top and the last book you place on the top of the stack is the first one you'll pick up. Similarly, in a stack data structure, elements are added or removed only from the top position.


LIFO (Last-In, First Out).

The Last In, First Out (LIFO) property of a stack refers to the characteristic where the most recently added item is the first one to be removed. In simpler terms, the element that is pushed (added) last onto the stack will be the first one to be popped (removed) from the stack.

Stack Operations
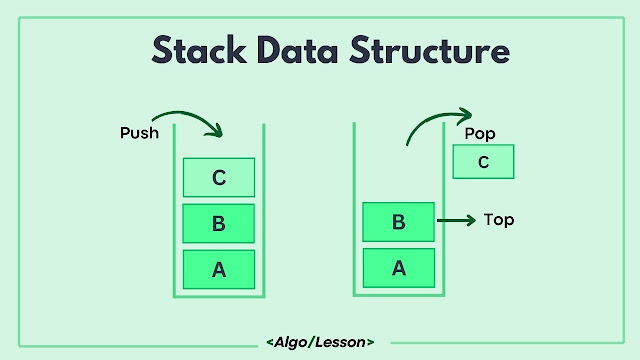Stack Data Structure

Basic Operation on Stack Data Structure.

There are certain functions and operations available for the stack data structure that are very useful for us.

  • push(): This function adds an element to the top of the stack. 
  • pop(): This function is used to remove the top element from the stack.
  • peek() or top(): This function is used to view the top element of the stack without removing it. 
  • isEmpty(): This function returns true if the stack is empty else, it returns false.
  • size(): This function returns the size of the stack.

Time Complexity of Stack Operations.

Function Time Complexity Explanation
push() O(1) Adding an element to the top of the stack takes constant time because it involves simply updating the top pointer or adding a new node.
pop() O(1) Removing an element from the top of the stack also takes constant time. It involves updating the top pointer or removing a node from the beginning of the linked list.
peek() O(1) Viewing the top element without removing it is a constant-time operation. It requires accessing the top element which can be done directly without iteration.
isEmpty() O(1) Checking if the stack is empty or not takes a constant amount of time because we just have to check if any element is present inside the stack or not.
size() O(1) Getting the size of the stack takes a constant amount of time because we already know the position of the top element which helps us to find the size of the stack.

Real-World Use of Stack Data Structure.

The principle of  Stack data structure is used in various scenarios:
  • Function Calls in Programming: When a function is called, its execution (variables, parameters, etc.) is added to the call stack. As functions complete execution, they are removed from the stack. This enables tracking the flow of the function calls and their respective return addresses.
  • Browser History: Navigating web pages creates a history, much like a stack. Each page visited is added to the history stack. The back button operates by removing the last page visited (the top of the stack).
  • Text Editor Undo Functionality: The undo feature in text editors uses a stack-like structure. Each action performed (typing, deleting, formatting) is recorded as a step in the stack. The undo operation reverses the most recent action by popping it off the stack.
  • Expression Evaluation: In programming, evaluating mathematical expressions involves using a stack. For instance, converting an infix expression (2 + 3) * 4 into a postfix uses a stack to maintain operator precedence.

Types of Stack.

There are two main types of stacks static and dynamic. 

Stack Stack: A static stack is a fixed-size stack, where the maximum capacity of the stack is determined and allocated during compile time. It is usually implemented using arrays due to their fixed-size characteristics. Once the size of the stack is defined, it cannot be changed during runtime.

Pros:

  • Easy to implement using arrays with fixed sizes.
  • Direct access to elements provides fast retrieval.
  • Predictable size allows for better memory management.
Cons:
  • Restricted to the predefined size, leading to potential overflow issues if the stack exceeds its capacity.
  • If the stack doesn't reach its full capacity, there might be wasted memory due to the fixed allocation.

Dynamic Stack: A dynamic stack adjusts its size dynamically during runtime based on the number of elements it holds. It is commonly implemented using dynamically allocated memory, like linked lists, to allow resizing.

Pros:

  • Accommodates varying numbers of elements without a predefined limit.
  • Efficiently utilizes memory by resizing as required.
  • Adjusts dynamically, minimizing the risk of overflow or underflow errors.
Cons:
  • More complex to implement compared to static stacks, especially when using linked lists.
  • Dynamic resizing operations may lead to memory fragmentation issues over time.

Implementation of Stack.

A stack can be implemented using other linear data structures like an array or linked list. Both have their own advantages and disadvantages. Let's discuss each of them one by one in detail. 

Pseudocode for Stack Implementation.

Stack Initialization:
    Stack[max_size]   // Initialize stack with a maximum size
    top = -1          // Initialize top pointer to -1 (empty stack)
    
Push(Stack, element):
    if top == max_size - 1:
        return "Overflow error"
    else:
        increment top
        Stack[top] = element

Pop(Stack):
    if top == -1:
        return "Underflow error"
    else:
        removed_element = Stack[top]
        decrement top
        return removed_element

Peek(Stack):
    if top == -1:
        return "Stack is empty"
    else:
        return Stack[top]

IsEmpty(Stack):
    return top == -1

Size(Stack):
    return top + 1

Stack Implementation Using Arrays.

Arrays offer a straightforward implementation for stacks. They provide direct access to elements using indices, making operations like push and pop relatively simple. Accessing elements by index allows faster retrieval of elements compared to linked lists, as arrays offer constant-time access.

Code Implementation:
// C++ Code implementation of stack operations
#include <iostream>
using namespace std;

const int MAX_SIZE = 100; // Maximum stack size

class StackArray {
private:
    int stack[MAX_SIZE];
    int top;

public:
    StackArray() {
        top = -1; // Initializing top to -1 for an empty stack
    }

    void push(int element) {
        if (top == MAX_SIZE - 1) {
            cout << "Stack Overflow" << endl;
            return;
        }
        top++;
        stack[top] = element;
    }

    int pop() {
        if (top == -1) {
            cout << "Stack Underflow" << endl;
            return -1; // Assuming -1 as an error value for an empty stack
        }
        int element = stack[top];
        top--;
        return element;
    }

    int peek() {
        if (top == -1) {
            cout << "Stack is empty" << endl;
            return -1; // Assuming -1 as an error value for an empty stack
        }
        return stack[top];
    }

    bool is_empty() {
        return top == -1;
    }

    int size() {
        return top + 1;
    }
};

int main() {
    StackArray stack;
    stack.push(5);
    stack.push(10);
    stack.push(15);

    cout << "Top of the stack: " << stack.peek() << endl;

    stack.pop();
    cout << "Top of the stack after pop: " << stack.peek() << endl;

    cout << "Is the stack empty? " << (stack.is_empty() ? "Yes" : "No") << endl;

    cout << "Current size of the stack: " << stack.size() << endl;

    return 0;
}

// Java code implementation of stack operations

public class StackArray {
  private int[] stack;
  private int top;
  private int maxSize;

  public StackArray(int maxSize) {
      this.maxSize = maxSize;
      this.stack = new int[maxSize];
      this.top = -1; // Initializing top to -1 for an empty stack
  }

  public void push(int element) {
      if (top == maxSize - 1) {
          System.out.println("Stack Overflow");
          return;
      }
      top++;
      stack[top] = element;
  }

  public int pop() {
      if (top == -1) {
          System.out.println("Stack Underflow");
          return -1; // Assuming -1 as an error value for an empty stack
      }
      int element = stack[top];
      top--;
      return element;
  }

  public int peek() {
      if (top == -1) {
          System.out.println("Stack is empty");
          return -1; // Assuming -1 as an error value for an empty stack
      }
      return stack[top];
  }

  public boolean isEmpty() {
      return top == -1;
  }

  public int size() {
      return top + 1;
  }

  public static void main(String[] args) {
      StackArray stack = new StackArray(5);
      stack.push(5);
      stack.push(10);
      stack.push(15);

      System.out.println("Top of the stack: " + stack.peek());

      stack.pop();
      System.out.println("Top of the stack after pop: " + stack.peek());

      System.out.println("Is the stack empty? " + (stack.isEmpty() ? "Yes" : "No"));

      System.out.println("Current size of the stack: " + stack.size());
  }
}

# Python code implementation of stack operations
class StackArray:
def __init__(self):
    self.MAX_SIZE = 100  # Maximum stack size
    self.stack = [None] * self.MAX_SIZE
    self.top = -1  # Initializing top to -1 for an empty stack

def push(self, element):
    if self.top == self.MAX_SIZE - 1:
        print("Stack Overflow")
        return
    self.top += 1
    self.stack[self.top] = element

def pop(self):
    if self.top == -1:
        print("Stack Underflow")
        return None  # Assuming None as an error value for an empty stack
    element = self.stack[self.top]
    self.top -= 1
    return element

def peek(self):
    if self.top == -1:
        print("Stack is empty")
        return None  # Assuming None as an error value for an empty stack
    return self.stack[self.top]

def is_empty(self):
    return self.top == -1

def size(self):
    return self.top + 1

# Test the StackArray class
stack = StackArray()
stack.push(5)
stack.push(10)
stack.push(15)

print("Top of the stack:", stack.peek())

stack.pop()
print("Top of the stack after pop:", stack.peek())

print("Is the stack empty?", "Yes" if stack.is_empty() else "No")

print("Current size of the stack:", stack.size())

// C# Code for stack implementation
using System;

public class StackArray {
    private int[] stack;
    private int top;
    private int maxSize;

    public StackArray(int maxSize) {
        this.maxSize = maxSize;
        this.stack = new int[maxSize];
        this.top = -1; // Initializing top to -1 for an empty stack
    }

    public void Push(int element) {
        if (top == maxSize - 1) {
            Console.WriteLine("Stack Overflow");
            return;
        }
        top++;
        stack[top] = element;
    }

    public int Pop() {
        if (top == -1) {
            Console.WriteLine("Stack Underflow");
            return -1; // Assuming -1 as an error value for an empty stack
        }
        int element = stack[top];
        top--;
        return element;
    }

    public int Peek() {
        if (top == -1) {
            Console.WriteLine("Stack is empty");
            return -1; // Assuming -1 as an error value for an empty stack
        }
        return stack[top];
    }

    public bool IsEmpty() {
        return top == -1;
    }

    public int Size() {
        return top + 1;
    }

    public static void Main() {
        StackArray stack = new StackArray(5);
        stack.Push(5);
        stack.Push(10);
        stack.Push(15);

        Console.WriteLine("Top of the stack: " + stack.Peek());

        stack.Pop();
        Console.WriteLine("Top of the stack after pop: " + stack.Peek());

        Console.WriteLine("Is the stack empty? " + (stack.IsEmpty() ? "Yes" : "No"));

        Console.WriteLine("Current size of the stack: " + stack.Size());
    }
}
Output:
Top of the stack: 15
Top of the stack after pop: 10
Is the stack empty? No
Current size of the stack: 2

Advantages of  Stack Implementation using Array:
  • Direct indexing in arrays enables quick element retrieval.
  • Arrays offer straightforward implementation of stacks.
  • They generally use less memory due to direct storage.

Disadvantages of Stack Implementation using Array:
  • Arrays have a limited size, hindering maximum capacity.
  • Adjusting array size is resource-intensive.
  • Unused space in arrays can lead to inefficiency.

Stack Implementation Using Linked_List.

Linked lists allow for dynamic memory allocation which helps us add many stack elements without a predetermined maximum capacity, which overcomes the limitation of fixed-size arrays. Unlike arrays, linked lists do not require resizing when accommodating more elements. Each new node can be dynamically allocated as needed.

Code Implementation:
// C++ code to implementation stack operation using linked list
#include <iostream>
using namespace std;

// Node structure to represent elements in the linked list
struct Node {
    int data;
    Node* next;
};

class StackLinkedList {
private:
    Node* top; // Pointer to the top node of the stack

public:
    StackLinkedList() {
        top = nullptr; // Initializing top to null for an empty stack
    }

    // Function to push an element onto the top of the stack
    void push(int element) {
        Node* newNode = new Node(); // Creating a new node
        newNode->data = element;
        newNode->next = top;
        top = newNode; // Updating top to point to the new node
    }

    // Function to pop an element from the top of the stack
    int pop() {
        if (top == nullptr) {
            cout << "Stack Underflow" << endl;
            return -1; // Assuming -1 as an error value for an empty stack
        }
        Node* temp = top;
        int element = temp->data;
        top = top->next;
        delete temp; // Freeing memory of the popped node
        return element;
    }

    // Function to peek at the top element without removing it
    int peek() {
        if (top == nullptr) {
            cout << "Stack is empty" << endl;
            return -1; // Assuming -1 as an error value for an empty stack
        }
        return top->data;
    }

    // Function to check if the stack is empty
    bool isEmpty() {
        return top == nullptr;
    }

    // Function to determine the size of the stack
    int size() {
        int count = 0;
        Node* current = top;
        while (current != nullptr) {
            count++;
            current = current->next;
        }
        return count;
    }
};

int main() {
    StackLinkedList stack;
    stack.push(5);
    stack.push(10);
    stack.push(12);
    stack.push(15);

    cout << "Top of the stack: " << stack.peek() << endl;

    stack.pop();
    cout << "Top of the stack after pop: " << stack.peek() << endl;

    cout << "Is the stack empty? " << (stack.isEmpty() ? "Yes" : "No") << endl;

    cout << "Current size of the stack: " << stack.size() << endl;

    return 0;
}

// Java code for stack implementation using linkedlist
public class StackLinkedList {
    private Node top;

    // Inner Node class
    private class Node {
        int data;
        Node next;

        Node(int data) {
            this.data = data;
            this.next = null;
        }
    }

    public StackLinkedList() {
        top = null;
    }
    // function to add element in the stack
    public void push(int element) {
        Node newNode = new Node(element);
        newNode.next = top;
        top = newNode;
    }
    // function to remove element from stack
    public int pop() {
        if (top == null) {
            System.out.println("Stack Underflow");
            return -1; // Assuming -1 as an error value for an empty stack
        }
        int element = top.data;
        top = top.next;
        return element;
    }
    // function to view top element of stack
    public int peek() {
        if (top == null) {
            System.out.println("Stack is empty");
            return -1; // Assuming -1 as an error value for an empty stack
        }
        return top.data;
    }
    // function to check if stack is empty
    public boolean isEmpty() {
        return top == null;
    }
    // function to get stack size
    public int size() {
        int count = 0;
        Node current = top;
        while (current != null) {
            count++;
            current = current.next;
        }
        return count;
    }

    public static void main(String[] args) {
        StackLinkedList stack = new StackLinkedList();
        stack.push(5);
        stack.push(10);
        stack.push(12);
        stack.push(15);

        System.out.println("Top of the stack: " + stack.peek());

        stack.pop();
        System.out.println("Top of the stack after pop: " + stack.peek());

        System.out.println("Is the stack empty? " + (stack.isEmpty() ? "Yes" : "No"));

        System.out.println("Current size of the stack: " + stack.size());
    }
}

# Python code implementation of stack using linked list 
class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class StackLinkedList:
    def __init__(self):
        self.top = None
    
    # function to add element in stack
    def push(self, element):
        new_node = Node(element)
        new_node.next = self.top
        self.top = new_node
    
    # function to remove element from the stack
    def pop(self):
        if self.top is None:
            print("Stack Underflow")
            return -1  # Assuming -1 as an error value for an empty stack
        element = self.top.data
        self.top = self.top.next
        return element
    
    # function to view top element of stack
    def peek(self):
        if self.top is None:
            print("Stack is empty")
            return -1  # Assuming -1 as an error value for an empty stack
        return self.top.data
    
    # function to check if stack is empty
    def is_empty(self):
        return self.top is None
    
    # function to get stack size
    def size(self):
        count = 0
        current = self.top
        while current is not None:
            count += 1
            current = current.next
        return count

# Test the StackLinkedList class
stack = StackLinkedList()
stack.push(5)
stack.push(10)
stack.push(12)
stack.push(15)

print("Top of the stack:", stack.peek())

stack.pop()
print("Top of the stack after pop:", stack.peek())

print("Is the stack empty?", "Yes" if stack.is_empty() else "No")

print("Current size of the stack:", stack.size())

// C# code implementation of stack using linked list
using System;

public class StackLinkedList {
    private Node top; // Top node of the stack

    // Node class representing elements in the linked list
    private class Node {
        public int data;
        public Node next;

        public Node(int data) {
            this.data = data;
            this.next = null;
        }
    }

    public StackLinkedList() {
        top = null; // Initializing top to null for an empty stack
    }
    // function to add element in stack
    public void Push(int element) {
        Node newNode = new Node(element); // Creating a new node
        newNode.next = top;
        top = newNode; // Updating top to point to the new node
    }

    // function to remove element from the stack
    public int Pop() {
        if (top == null) {
            Console.WriteLine("Stack Underflow");
            return -1; 
        }
        int element = top.data;
        top = top.next;
        return element;
    }

    // function to view top element of stack
    public int Peek() {
        if (top == null) {
            Console.WriteLine("Stack is empty");
            return -1; 
        }
        return top.data;
    }
    
    // function to check if stack is empty
    public bool IsEmpty() {
        return top == null;
    }

    // function to get the size of the stack
    public int Size() {
        int count = 0;
        Node current = top;
        while (current != null) {
            count++;
            current = current.next;
        }
        return count;
    }

    public static void Main() {
        StackLinkedList stack = new StackLinkedList();
        stack.Push(5);
        stack.Push(10);
        stack.Push(12);
        stack.Push(15);

        Console.WriteLine("Top of the stack: " + stack.Peek());

        stack.Pop();
        Console.WriteLine("Top of the stack after pop: " + stack.Peek());

        Console.WriteLine("Is the stack empty? " + (stack.IsEmpty() ? "Yes" : "No"));

        Console.WriteLine("Current size of the stack: " + stack.Size());
    }
}
Output:
Top of the stack: 15
Top of the stack after pop: 12
Is the stack empty? No
Current size of the stack: 3

Advantages of Stack Implementation using Linked List.
  • Linked lists adapt to varying element counts without a fixed maximum limit.
  • They don't have predefined size limitations, offering flexibility.
  • Allocate memory as needed, minimizing wastage.
  • Allows efficient element addition/removal without resizing.

Disadvantages of Stack Implementation using Linked List.
  • Extra memory is used for maintaining pointers.
  • Sequential access impacts direct element retrieval.
  • Traversal can be slower for larger lists.

Both implementations follow the same fundamental principles of maintaining the LIFO behavior and providing operations for manipulating the stack. You can also check the comparison between stack and queue data structures to understand the situation in which we use Stacks.

⚡ Please share your valuable feedback and suggestion in the comment section below or you can send us an email on our offical email id ✉ algolesson@gmail.com. You can also support our work by buying a cup of coffee ☕ for us.

Similar Posts

No comments:

Post a Comment


CLOSE ADS
CLOSE ADS