Depth First Search (DFS) is a graph traversal algorithm that explores a graph by visiting as far as possible along each branch before backtracking. It starts from a given source vertex and recursively explores all of its neighbors, marking each vertex as visited as it traverses the graph. Once it reaches the end of a branch, it backtracks to the last unexplored vertex and continues the search.
Algorithm for Depth First Search.
- Step 1: Create a visited array and initialize it to false.
- Step 2: Initialize a stack and push the source vertex onto it.
- Step 3: While the stack is not empty, do the following:
- a. Pop a vertex from the stack.
- b. If the vertex has not been visited, mark it as visited and do the following:
- i. Process the vertex (e.g., print its value).
- ii. Get its neighbors and push them onto the stack.
- Step 4: Repeat step 3 until the stack is empty.
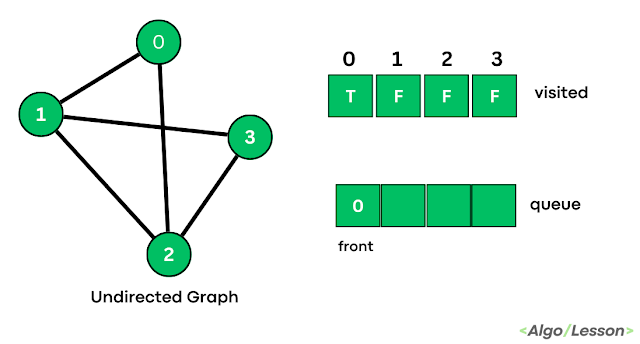
Example with Illustration.
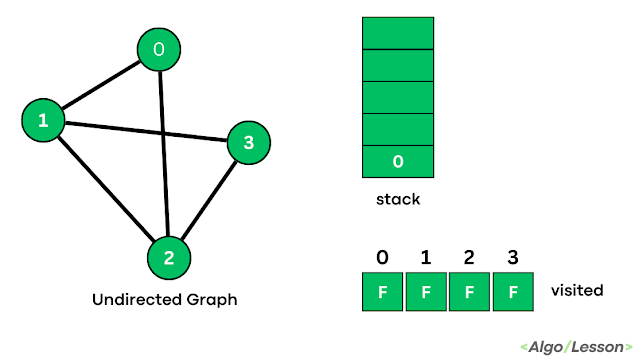 |
| Step 1 |
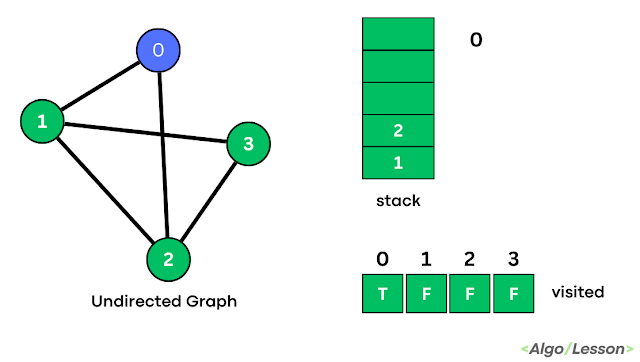 |
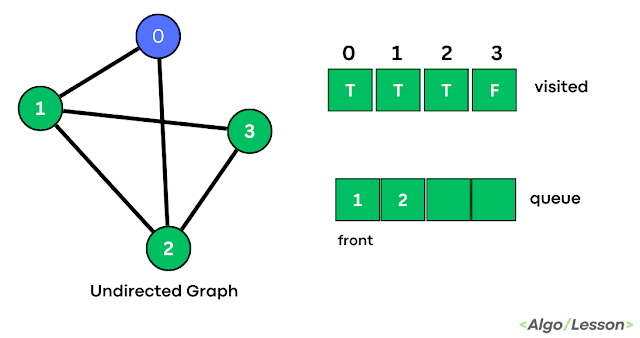
| Step 2 |
 |
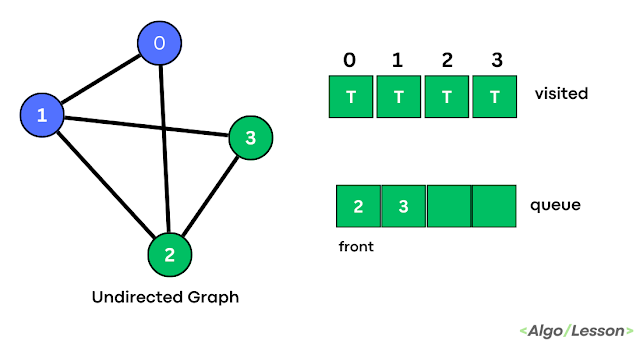
| Step 3 |
Pop the top element of the stack that is 2 and mark that index as visited in the visited array and print it. Push all other neighbor vertices of 2 inside the stack if already not visited.
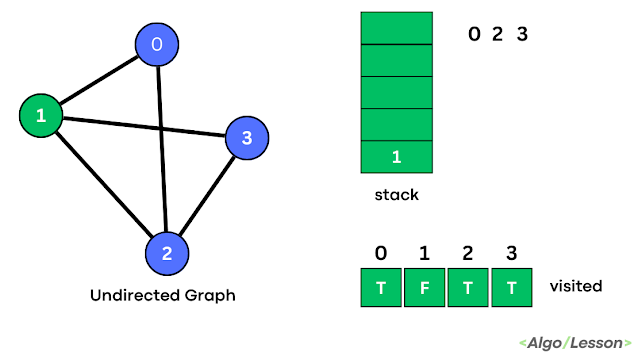 |
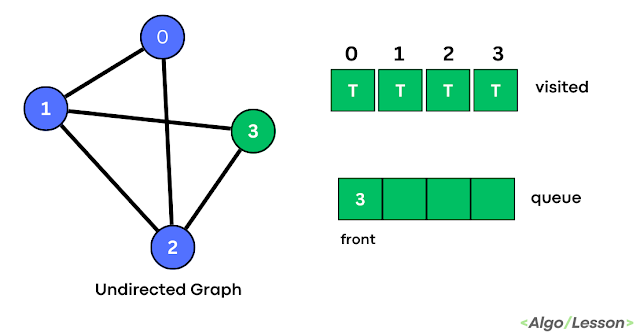
| Step 4 |
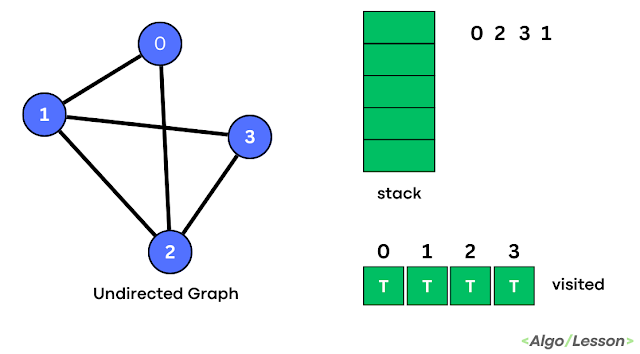 |
| Step 5 |
C++ code for DFS (Depth First Search) Traversal using Stack.
//C++ code implementation for DFS Traversal of graph using Stack #include <iostream> #include <vector> #include <stack> using namespace std; //function for dfs void DFS(int V, vector<int> graph[], int start, vector<bool>& visited) { stack<int> s; s.push(start); while (!s.empty()) { int v = s.top(); s.pop(); if (!visited[v]) { visited[v] = true; cout << v << " "; for (int u : graph[v]) { s.push(u); } } } } int main() { int V = 4; vector<int> graph[V]; graph[0] = {1, 2}; graph[1] = {0, 2, 3}; graph[2] = {0, 1, 3}; graph[3] = {1, 2}; vector<bool> visited(V, false); DFS(V, graph, 0, visited); return 0; }
0 2 3 1- Time Complexity: O(V + E) where V is the number of vertices and E is the number of Edges. Each vertex and each edge is explored exactly once.
- Space Complexity: O(V + E) as it uses a stack to keep track of vertices and an array to mark visited vertices. In the worst case, the stack will store all vertices of the longest path, which is the maximum the maximum depth of the recursion.
Algorithm for Depth First Search (Recursive).
- Step 1: Create a visited array and initialize it to false.
- Step 2: Call the DFS function with the starting vertex as the argument.
- Step 3: In the DFS function, mark the current vertex as visited and process it (e.g., print its value).
- Step 4: For each unvisited neighbor of the current vertex, recursively call the DFS function with the neighbor as the argument.
//C++ code implementation for DFS Traversal of graph using Recursion #include <iostream> #include <vector> #include <stack> using namespace std; //function for dfs void DFS(int V, vector<int> graph[], int start, vector<bool>& visited) { visited[start] = true; cout << start << " "; for (int u : graph[start]) { if (!visited[u]) { DFS(V, graph, u, visited); } } } int main() { int V = 4; vector<int> graph[V]; graph[0] = {1, 2}; graph[1] = {0, 2, 3}; graph[2] = {0, 1, 3}; graph[3] = {1, 2}; vector<bool> visited(V, false); DFS(V, graph, 0, visited); return 0; }
0 1 2 3- Time Complexity: O(V + E) where V is the number of vertices and E is the number of Edges.
- Space Complexity: O(V) as an array to mark visited vertices. The maximum depth of the recursion is the number of vertices.