Binary Search Algorithm in Python.

There are two popular searching algorithms to find a target value in an Array 'Linear Search' and 'Binary Search'. In this article, we will learn about the Binary Search Algorithm in detail using Python Programming.

Binary Search Algorithm.

Binary search is an efficient algorithm for finding an item from a sorted list of items. It works by repeatedly dividing the search interval in half. The only drawback of this search algorithm is that we need a sorted array to perform our search operation to find the target element in the given list. 

Below are the algorithm steps to follow:

Step 1: Set two pointers, low and high, to the start and end of the array, respectively.

Step 2: Loop until the base case is reached:

• Calculate the middle index as (low + high) // 2.

• If the element at the middle index is equal to the target, return the index.

• If the element is greater than the target, update high to mid - 1 and repeat the search in the left half.

• If the element is smaller than the target, update low to mid + 1 and repeat the search in the right half.

Step 3: If low is greater than high, the target is not present. Return -1.

Example of Binary Search:

Let's go through an example to understand the workings of the Binary Search Algorithm.

We have a sorted array [1, 3, 5, 7, 9, 11, 13, 15, 17, 19], and we want to find the index of element 13.

Initialize Pointers: Set low to 0 and high to 9 (the indices of the array's first and last elements).

Iteration 1:

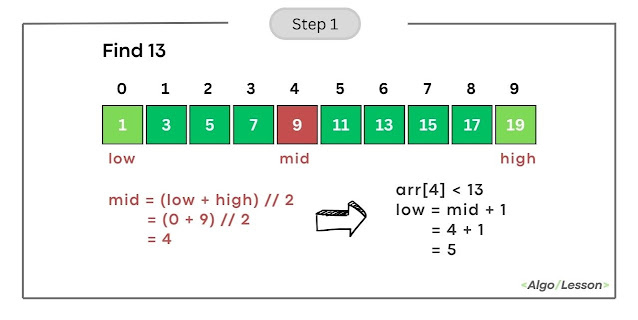
• Calculate mid as (low + high) // 2 = (0 + 9) // 2 = 4.
• Compare arr[mid] (element at index 4) with the target (13).
• Since arr[4] is less than 13, update low to mid + 1, making low = 5.

Iteration 2:

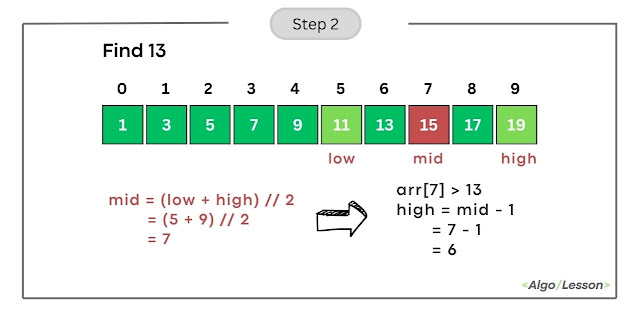
• Calculate mid as (low + high) // 2 = (5 + 9) // 2 = 7.
• Compare arr[mid] (element at index 7) with the target (13).
• Since arr[7] is greater than 13, update high to mid-1, making high = 6.

Iteration 3:

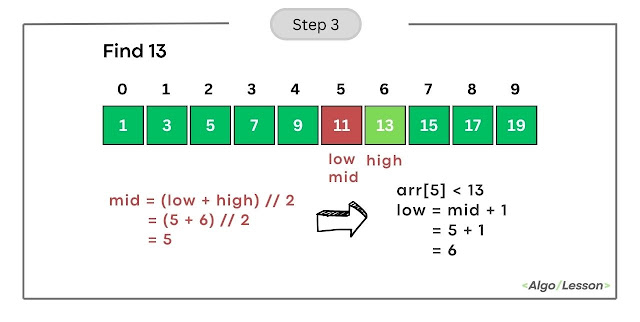
• Calculate mid as (low + high) // 2 = (5+ 6) // 2 = 5.
• Compare arr[mid] (element at index 5) with the target (13).
• Since arr[5] is less than 13, update low to mid + 1, making low = 6.

Iteration 4:

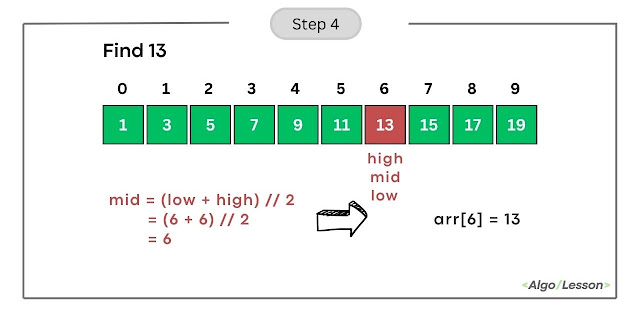
• Calculate mid as (low + high) // 2 = (6 + 6) // 2 = 6.
• Compare arr[mid] (element at index 6) with the target (13).
• Since arr[6] is equal to 13, we found the target. Return the index 6.

The target element 13 is present at index 9 in the array.

Python Program for Binary Search Using Iteration.

# Python code for Iterative Binary Search to find
# target element from sorted array
def binary_search(arr, target):
    low, high = 0, len(arr) - 1
    
    while low <= high:
        mid = (low + high) // 2
        mid_element = arr[mid]

        if mid_element == target:
            return mid
        elif mid_element < target:
            low = mid + 1
        else:
            high = mid - 1

    return -1

# Example
sorted_array = [1, 2, 3, 4, 5, 6, 7, 8, 9]
target_element = 6
result = binary_search(sorted_array, target_element)

if result != -1:
    print(f"Element {target_element} is present at index {result}.")
else:
    print(f"Element {target_element} is not present in the array.")

Output:

Element 6 is present at index 5.

• Time Complexity: The time complexity of binary search is O(log n), where 'n' is the number of elements in the array.

• Space Complexity: The space complexity is O(1), indicating that the memory used by the algorithm remains constant regardless of the input size.

Python Program for Binary Search Using Recursion.

# Python code for Recursive Binary Search Algorithm
def binary_search_recursive(arr, low, high, target):
    if low <= high:
        mid = (low + high) // 2

        # Check if the target is present at the middle
        if arr[mid] == target:
            return mid
        # If the target is smaller, search in the left half
        elif arr[mid] > target:
            return binary_search_recursive(arr, low, mid - 1, target)
        # If the target is larger, search in the right half
        else:
            return binary_search_recursive(arr, mid + 1, high, target)
    else:
        # Target is not present in the array
        return -1

# Example usage:
arr = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
target = 13
result = binary_search_recursive(arr, 0, len(arr) - 1, target)

if result != -1:
    print(f"Element {target} is present at index {result}.")
else:
    print(f"Element {target} is not present in the array.")

Output:

Element 13 is present at index 6.

The base case of the above recursive function is when low is greater than high, indicating that the search range is empty. The function will return the index at which the element is present else it will return -1 which means the target element is not present in the given array.

• Time Complexity: The time complexity is O(log n) because, at each step, the search range is divided by 2.

• Space Complexity: The space complexity is O(log n) due to the recursive call stack.

Linear Search Algorithm in Python.

Given an integer array arr[] of size n and an element x, the task is to write a Python program to search for the element x in the given array.

Example:

Input: arr = [12, 10, 9, 11, 41] x = 9
Output: X is present at index 2.

Input: arr = [1, 2, 3, 4, 6, 9] x = 7
Output: Not Found

Input: arr = [-1, 2, 4] x = 2
Output: X is present at index 1

There are two popular algorithms one is Linear Search and another is Binary Search for searching an element in an array. In this article, we are going to learn how to use the Linear Search algorithm in Python programming.

Linear Search Algorithm.

Linear search, also known as sequential search, is a straightforward searching algorithm where we start from the beginning of the array and compare each element with the target value until a match is found or the entire array has been traversed.

 

Below are the algorithm steps to do the linear search:

• Step 1: Start from the first element of the array.

• Step 2: Compare the current element with the target value x.

• Step 3: If the element is equal to the target x, return the index.

• Step 4: If not, move to the next element.

• Step 5: Repeat steps 2-4 until the target is found or the end of the array is reached.

• Step 6: If the target is not found after traversing the entire array, return -1.

Python Program for Linear Search.

Below is the Python code implementation of Linear search using an iterative method.

# Python code to search element using Linear Search
def linear_search(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i  # Target found, return the index
    return -1  # Target not found

# Example usage
array = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5]
target_value = 6
result = linear_search(array, target_value)

if result != -1:
    print(f'Target {target_value} found at index {result}.')
else:
    print(f'Target {target_value} not found in the array.')

Output:

Target 6 found at index 7.

• Time Complexity: The worst-case time complexity is O(n) when the target element is present at the end of the array. 

• Space Complexity: O(1) - Linear search is an "in-place" algorithm that doesn't require additional memory proportional to the input size.

Python Program for Linear Search Using Recursion.

In this recursive algorithm, we have two base cases: first, if the current element equals the target, it returns the current index; second, if the current index surpasses the array length, indicating the target is not present, it returns -1. 

In the recursive case, the function calls itself with an incremented index to continue the search in the remaining array. This process repeats until one of the base cases is met.

Below is the Python code implementation of Linear search using recursion.

Python Code.

# Python program to search element using Recursive Method
def linear_search(arr, target, current_index=0):
    # Base case: target found
    if current_index < len(arr):
        if arr[current_index] == target:
            return current_index
    
    # Base case: target not found
    if current_index == len(arr):
        return -1
    
    # Recursive case: search in the remaining array
    return linear_search_recursive(arr, target, current_index + 1)

# Example
arr = [1, 2, 3, 4, 5]
target = 3

result = linear_search(arr, target)

if result != -1:
    print(f"Target {target} found at index {result}.")
else:
    print(f"Target {target} not found in the array.")

Output:

Target 3 found at index 2.

• Time Complexity: Linear search has a time complexity of O(n) in the worst case.
• Space Complexity: The recursive calls use the call stack, and in the worst case, the space complexity is O(n) due to the depth of the recursion. 

Program to Find the Smallest and Largest Element of an Array.

Given an array of sizes n and we need to find the maximum and minimum number present in the given array.

Example:

Input: arr[] = {12, 9, 2, 7, 3, 10}
Output: 

Maximum: 12

Minimum: 2

Input: arr[] = {5, 9, -2, 23, 7, 10}
Output: 

Maximum: 23
Minimum: -2

Approach 1: Brute Force approach.

In this approach, we traverse the entire array and pick each element one by one to compare the smallest and largest element. 

Following steps to solve the problem:

1. Declare two variables max_value and min_value and initialize max_value with 2. INT_MIN and min_value with INT_MAX.

3. Traverse the array and

• Update the value of max_value if you found any value greater than the current max_value. 
• Update the value of min_value if you found any value greater than the current min_value. 

4. Print maximum and minimum values.

Below is the C++ code Implementation:

//C++ code to find the maximum and minimum value of an array
#include<iostream>
using namespace std;

//function to print maximum and minimum value
void largeSmall(int arr[], int n){
   int max_value = INT_MIN;
   int min_value = INT_MAX;

   for(int i = 0; i < n; i++){
    //checking max value
    if(arr[i] > max_value)
       max_value = arr[i];
    //checking min value   
    if(arr[i] < min_value)
       min_value = arr[i];   
   }

   cout<<"Maximum: "<<max_value<<endl;
   cout<<"Minimum: "<<min_value<<endl;
}

int main(){
    
    int arr[] = {12, 9, -2, 7, 3, 10};
    //size of the given array
    int n = sizeof(arr)/sizeof(arr[0]);
    //function call
    largeSmall(arr, n);
    return 0;
}

Output:

Maximum: 12
Minimum: -2

• Time Complexity: O(n)
• Space Complexity: O(1)

Approach 2: Using Recursion.

1. In the recursive approach, we made two different function call for maximum and minimum. 

if(n == 1) 

   return arr[0]

2. This is our base case which indicates that when you traverse the complete array and only one element is left in the array then we can simply return arr[0].

3. Recursively we are reducing the size of the array in each recursive call (n-1) and trying to store the maximum so far.  

Below is the C++ code Implementation:

//C++ Recursive code to find the maximum and minimum value of an array
#include<iostream>
using namespace std;

//recursive function to return maximum value
int largestNum(int arr[], int n){
  //base case when we traverse the complete array
  if(n == 1)
    return arr[0];

  return max(arr[n-1], largestNum(arr, n-1));  
}

//recursive function to return the minimum value
int smallestNum(int arr[], int n){
  //base case when we traverse the complete array
  if(n == 1)
    return arr[0];

  return min(arr[n-1], smallestNum(arr, n-1));  
}

int main(){
    
    int arr[] = {12, 9, -2, 7, 3, 10};
    //size of the given array
    int n = sizeof(arr)/sizeof(arr[0]);
    //function call
    cout<<"Maximum: "<<largestNum(arr, n)<<endl;
    cout<<"Minimum: "<<smallestNum(arr, n)<<endl;
    return 0;
}

Output:

Maximum: 12
Minimum: -2

• Time Complexity: O(n)
• Space Complexity: O(1)

Approach 3: Using Library Function.

In most programming languages there are several built-in functions to use for finding the maximum and minimum of an array. In C++ we have max_element() and min_element() library function.

Below is the C++ code Implementation:

//C++ code to find maximum and minimum value of an array
#include<bits/stdc++.h>
using namespace std;

//library function to return maximum value
int largestNum(int arr[], int n){
    return *max_element(arr, arr+n);
}

//library function to return minimum value
int smallestNum(int arr[], int n){
  return *min_element(arr, arr+n);
}

int main(){
    
    int arr[] = {12, 9, -2, 7, 3, 10};
    //size of given array
    int n = sizeof(arr)/sizeof(arr[0]);
    //function call
    cout<<"Maximum: "<<largestNum(arr, n)<<endl;
    cout<<"Minimum: "<<smallestNum(arr, n)<<endl;
    return 0;
}

Output:

Maximum: 12
Minimum: -2

• Time Complexity: O(n)
• Space Complexity: O(1)

Also see:

(getButton) #text=(Program to Find Kth Largest Element of an Array) #icon=(link) #color=(#2339bd)

(getButton) #text=(Program to Find Kth Smallest Element of an Array) #icon=(link) #color=(#2339bd)

Program to Find Kth Smallest Element of an Array.

Given an array of n distinct elements and we need to find the kth smallest element from the given array where the value of k is larger than the size of the given array.

Example:

Input: arr[] = {12, 9, 2, 7, 3, 10}, k = 2
Output: 3

Input: arr[] = {12, 9, 2, 7, 3, 10}, k = 5
Output: 10

There are multiple ways in which you can solve this basic level array problem and here we are going to discuss two different ways to find the kth smallest element of an array. 

Approach 1: Using Sorting.

The brute force approach that we can think of is to sort the given array in ascending order and return the element present at index (k-1) and array elements are stored based on 0-based indexing. You can use the Quick sort algorithm to sort the array whose time complexity is O(nlogn).

In C++, we have one sort member function that sorts the array in ascending order by default and the internally implemented quick sort algorithm. 

C++ Code Implementation:

//C++ code to find the kth smallest element of an array
#include<iostream>
#include<algorithm>
using namespace std;

//function to return kth smallest element
int smallestNumber(int arr[], int n, int k){
    //sort the array
    sort(arr, arr+n);

    return arr[k-1];
}

int main(){
    
    int arr[] = {12, 9, 2, 7, 3, 10};
    //size of given array
    int n = sizeof(arr)/sizeof(arr[0]);
    int k = 2;
    cout<<"The kth smallest element is: "<<smallestNumber(arr, n, k); 

    return 0;
}

Output:

The kth smallest element is: 3

• Time Complexity: O(nlogn)
• Space Complexity: O(1)

Approach 2: Using Set data structure.

The set data structure is used to store unique elements of same type in sorted order. As mentioned in the question itself that all elements are distinct which means if we store them in a set data structure we can easily find the kth smallest element. 

• The drawback of using set data structure is that we required n extra spaces to sort the given array which increase the space complexity to O(n).

C++ Code Implementation:

//C++ code to find kth smallest element of an array using set
#include<bits/stdc++.h>
using namespace std;

//function to return kth smallest element
int smallestNumber(int arr[], int n, int k){
    //set data structure
    set<int> s(arr, arr+n);
    //pointer to first element
    set<int>::iterator it = s.begin();
    advance(it, k-1);

    return *it;
}

int main(){
    
    int arr[] = {12, 9, 2, 7, 3, 10};
    //size of given array
    int n = sizeof(arr)/sizeof(arr[0]);
    int k = 5;
    cout<<"The kth smallest element is: "<<smallestNumber(arr, n, k); 

    return 0;
}

Output:

The kth smallest element is: 10

• Time Complexity: O(nlogn)
• Space Complexity: O(n)

Next: (getButton) #text=(Program to Find Kth Largest Element of an Array) #icon=(link) #color=(#2339bd)

Program to Find Kth Largest Element of an Array.

Given an array of n distinct elements and we need to find the kth largest number from the given array where the value of k is larger than the size of the given array.

Example:

Input: arr[] = {4, 9, 2, 7, 3, 10}, k = 3
Output: 7

Input: arr[] = {4, 9, 2, 7, 3, 10}, k = 5
Output: 3

Approach 1: Using Sorting.

The simplest approach that anyone can think of is to sort the given array in ascending order and return the element present at index (n-k) and array elements are stored based on 0-based indexing. You can use the sort function given in almost all programming languages or you can use quick sort whose time complexity is O(nlogn).

C++ Code Implementation:

//C++ code to find the kth largest element of an array
#include<iostream>
#include<algorithm>
using namespace std;

//function to return kth largest element
int largestNumber(int arr[], int n, int k){
    //sort the array
    sort(arr, arr+n);

    return arr[n-k];
}

int main(){
    
    int arr[] = {4, 9, 2, 7, 3, 10};
    //size of given array
    int n = sizeof(arr)/sizeof(arr[0]);
    int k = 3;
    cout<<"The kth largest element is: "<<largestNumber(arr, n, k); 

    return 0;
}

Output:

The kth largest element is: 7

• Time Complexity: O(nlogn)
• Space Complexity: O(1)

Approach 2: Using Set data structure.

The set data structure is used to store unique elements same type in sorted order. As mentioned in the question itself that all elements are distinct which means if we store them in a set data structure we can easily find the kth largest element.

C++ Code Implementation:

//C++ code to find kth largest element of an array using set
#include<bits/stdc++.h>
using namespace std;

//function to return kth largest element
int largestNumber(int arr[], int n, int k){
    //set data structure
    set<int> s(arr, arr+n);
    //pointer to first element
    set<int>::iterator it = s.begin();
    advance(it, n-k);

    return *it;
}

int main(){
    
    int arr[] = {4, 9, 2, 7, 3, 10};
    //size of given array
    int n = sizeof(arr)/sizeof(arr[0]);
    int k = 2;
    cout<<"The kth largest element is: "<<largestNumber(arr, n, k); 

    return 0;
}

Output:

The kth largest element is: 9

• Time Complexity: O(nlogn)
• Space Complexity: O(n)

Next: (getButton) #text=(Program to Find Kth Smallest Element of an Array) #icon=(link) #color=(#2339bd)

Binary Search Algorithm with code in C++.

Binary Search is one the most popular and widely used search algorithms used to search whether a particular element is present in the given sorted array or not. It is much better than the Linear search algorithm because it is much faster.  

Problem: Given a sorted array of integers arr[ ] of size n and a target element x, write a C++ program to search the position of x in the given array.

Input: arr[ ] = {7, 10, 11, 15, 20, 30, 26}   x = 20

Output: 4
x is present at index 4.

Input: arr[ ] = {11, 15, 22, 30, 35, 43, 60, 75, 120}   x = 65

Output: -1
x is not present in the arr[ ].

Binary Search Explanation. 

When you try to find the target element in the given array, the worst-case scenario is that when you have to check each element of the given array and it leads to O(n) time complexity. But when the array elements are arranged in sorted order, you can use this extra information to reduce the time complexity to O(log n). 

• If you use a binary search on 100 elements to find your target, the worst-case scenario would be 10 searches. Can you imagine a huge performance improvement? 😲

You get this huge performance improvement because, for each iteration, you reduce the number of elements you will be looking at in half. The idea is to compare the target element to the middle element of the array. 

• If you find the target element is equal to the middle element, return the position of the middle element and stop.
• If the target element is smaller than the middle element, continue searching on the left side of the middle element. high = mid-1
• If the target element is greater than the middle element, continue searching on the right side of the middle element. low = mid+1
• Repeat all three steps until you find the matching element else return -1.

Example: C++ code for Binary Search Algorithm.

#include <iostream>
using namespace std;

int binarySearch(int arr[], int n, int key)
{ 

    int low = 0, high = n - 1; 

    while (low <= high)
    {
        int mid = low + (high - low) / 2;
        //target is found
        if (arr[mid] == key)
        {
            return mid;
        }
        else if (arr[mid] < key) //target might be present in right half
        {
            low = mid + 1;
        }
        else    //target might be present in left half
        {
            high = mid - 1;
        }
    }
    return -1;
}

int main()
{

    int arr[] = {7, 10, 11, 15, 20, 30, 36};
    // size of given array
    int size = sizeof(arr) / sizeof(arr[0]);
    // target element to be find
    int x = 20;

    int index = binarySearch(arr, size, x);
    if (index == -1)
    {
        cout << "Value is not present in the given array." << endl;
    }
    else
    {
        cout << "Value present at index: " << index << endl;
    }
}

Output:

Value present at index: 4

• Time Complexity: O(log n)
• Space Complexity: O(1)

Important points to note: 

int low = 0, high = n - 1;

low and high work like a boundary and we will be looking at elements inside the boundary to find out the target element x and these boundaries get change with each iteration until we found our target loop gets terminated when low == high.

int mid = (high + low) / 2; //formula 1 
int mid = low + (high - low) / 2; //formula 2

Now, a few of you might be thinking that why we are using formula 2 instead of formula 1 as both the formula is going to give the same result? The answer to this question is to avoid integer overflow as the maximum value the integer datatype can hold is 2147483647.  So when you in case of adding two bigger numbers and try to store them in integer datatype it will give you a wrong answer. 

I believe the remaining part of the code was easy to understand with the help of the above explanation and animation gif. If you have any questions or suggestions related to the post, you can share them with us in the comment section below.