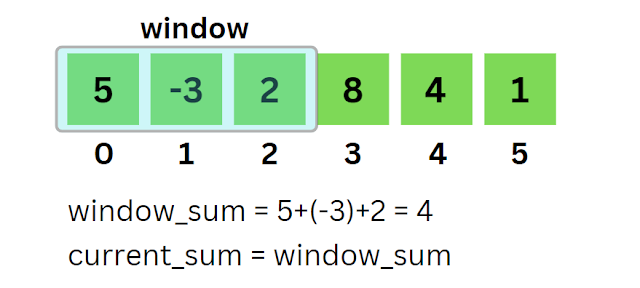
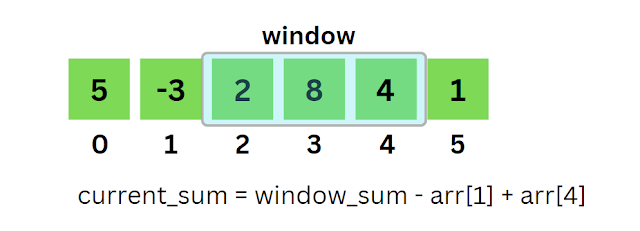
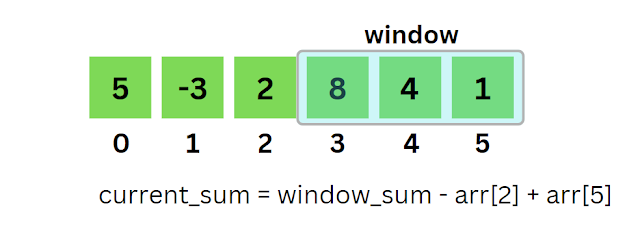
Sliding Window is an efficient approach to solve problems involving contiguous subarrays. It can be used to find the maximum or minimum sum of a contiguous subarray of size k. This approach involves maintaining a "window" that moves from the left to the right of the array, keeping track of the sum of the elements within the window.
Variable Size Sliding Window.
The Variable Size Sliding Window Algorithm, also known as Dynamic Sliding Window, is a technique used for efficiently processing arrays or lists to avoid unnecessary re-computation. Unlike the Fixed Size Sliding Window, where the window size remains constant, the Variable Size Sliding Window allows the window to dynamically adjust its size based on certain conditions.
Approach of Variable Size Sliding Window:
In this approach, we use two pointers left and right to define the window size. We move our right pointer to expand the window size until a certain condition is violated. Similarly, we move our left pointer to shrink the size of the window to the desired condition. Each time we either store a result or perform some computation whenever the size of the window is changed. We repeat these steps until the right pointer reaches the end of the array.
Let's understand the working of the Variable Size Sliding Window Algorithm with an example problem.
Example to Illustrate the Dynamic Sliding Window Technique.
Problem: Given an array of positive integer nums and a positive integer target, find the minimum length of a contiguous subarray whose sum is greater than or equal to the target. If no such subarray exists, return 0.
Example:
Input: num[] = {2, 3, 1, 2, 4, 3} target = 7
Output: 2
Explanation: The subarray [4,3] has the minimum length
among the contiguous subarrays whose sum is greater than or equal to 7.
There are multiple approaches to solving this problem but here we will focus on the sliding window approach.
Algorithm:
Below are the steps to follow to solve this problem:
Step 1: We initialize a variable, 'minLen', to hold the minimum length of the contiguous subarray found so far. We also initialize a variable, 'sum', to keep track of the sum of the elements in the current window.
Step 2: We iterate over the input array, using a for loop to iterate through each element. For each element, we add its value to the 'sum' variable.
Step 3: Inside the for loop, we check if the 'sum' is greater than or equal to the target. If it is, we update the 'minLen' variable to be the minimum of its current value and the current window's length (calculated using the 'right' pointer).
Step 4: After updating the 'minLen' variable, we slide the window to the right by subtracting the first element of the current window from the 'sum' variable. This involves incrementing the 'left' pointer by 1.
Step 5: We repeat steps 3-4 until the 'right' pointer reaches the end of the input array.
Step 6: Finally, we return the value of the 'minLen' variable, which represents the minimum length of the contiguous subarray whose sum is greater than or equal to the target.
Below is the code implementation of the Variable size Sliding Window problem.
C++ Code:
// C++ code implementation of finding the minimum length //of the subarray for given sum #include <iostream> #include <vector> #include <climits>
using namespace std;int minSubarrayLen(int target, vector<int>& nums) { int n = nums.size(); int left = 0, right = 0; int minLen = INT_MAX; int sum = 0; while (right < n) { sum += nums[right]; while (sum >= target) { minLen = min(minLen, right - left + 1); sum -= nums[left]; left++; } right++; } return (minLen == INT_MAX) ? 0 : minLen; } int main() { vector<int> nums = {2, 3, 1, 2, 4, 3}; int target = 7; cout << minSubarrayLen(target, nums) << endl; return 0; }
2
Java Code:
// Java code to find minimum length subarray // for the given target public class VariableSizeSlidingWindow { public static int minSubArrayLen(int target, int[] nums) { int left = 0, right = 0, sum = 0; int minLength = Integer.MAX_VALUE; while (right < nums.length) { sum += nums[right]; while (sum >= target) { minLength = Math.min(minLength, right - left + 1); sum -= nums[left]; left++; } right++; } return minLength == Integer.MAX_VALUE ? 0 : minLength; } public static void main(String[] args) { int[] nums = {2, 3, 1, 2, 4, 3}; int target = 7; int result = minSubArrayLen(target, nums); System.out.println("Minimum Length: " + result); } }
Minimum Length: 2- Time Complexity: The time complexity is O(n), where n is the length of the input array. This is because each element in the array is processed exactly once.
- Space Complexity: The space complexity is O(1), as we only use a constant amount of space to store the necessary variables.
