Maximum Depth of Nested Parenthesis.

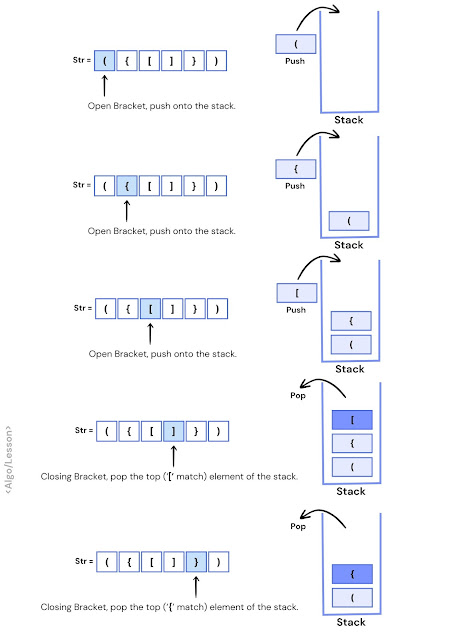
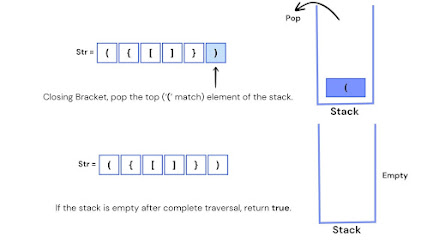
Given a string consisting of opening and closing parentheses, find the maximum depth of nested parentheses. The depth of a valid nested parentheses expression is defined as the number of parenthesis pairs that are properly nested. Implement a function that takes a string as input and returns the maximum depth of nested parentheses.

• The input string s consists of parentheses characters '(' and ')' only.
• The length of s is between 1 and 1000.

Example:

Input: "(A)"

Output: 1

Explanation: The depth of the parentheses is 1.

Input: "((A+B))+(A(B-(C*D)))"

Output: 3

Explanation: The depth of the parentheses is 3.

You might have already guessed that this problem is a standard stack-based problem in which we have to find the maximum depth of the nested parenthesis. In this article, I will explain two different approaches to solving this problem one is of course using stack and another solution is without using any additional data structure. 

Maximum Depth of Nested Parenthesis using Stack.

In this approach, we use a stack to track the depth of the parenthesis at any particular moment while traversing the given parenthesis string. We will also keep a variable to keep updating the maximum depth whenever we meet a closing parenthesis.

Algorithm Steps:

• Initialize an empty stack to keep track of opening parenthesis.
• Create a variable count and initialize it with 0, it will store the maximum depth of nested parenthesis.
• Traverse the given input string and follow the below steps:
• If the character is opening parenthesis '(' then push it into the stack.
• If the character is a closing parenthesis ')' then update the value of the count if it is less than the current stack size. Pop an element from the stack.
• Return the count variable as the maximum depth of parenthesis.

Below is the code implementation of the above approach:

C++ Java Python C#

// C++ code to find the maximum depth
// of nested parenthesis 
#include <iostream>
#include<stack>
using namespace std;

int maxDepth(string str) {
    stack<char> st;
    int count = 0;

    for(char c:str) {
        if(c == '(') {
            // insert the opening parenthesis 
            st.push(c);
        }else if(c == ')'){
            // update the max depth 
            if(count < st.size()) {
                count = st.size();
            }
            st.pop();
        }
    }
    return count;
}
int main() {
    string str = "((A+B))+(A(B-(C*D)))";

    int result = maxDepth(str);

    cout<< "Maximum Depth: " <<result <<endl;
    return 0;
}

// Java code implementation to find maximum
// depth of nested parenthesis
import java.util.Stack;

public class Main {
    public static void main(String[] args) {
        String str = "((A+B))+(A(B-(C*D)))";

        int result = maxDepth(str);

        System.out.println("Maximum Depth: " + result);
    }

    public static int maxDepth(String str) {
        Stack<Character> st = new Stack<>();
        int count = 0;

        for (char c : str.toCharArray()) {
            // insert the opening parenthesis in stack 
            if (c == '(') {
                st.push(c);
            } else if (c == ')') {
                // update the max depth
                if (count < st.size()) {
                    count = st.size();
                }
                st.pop();
            }
        }

        return count;
    }
}

# Python code to find the max depth of parenthesis
def max_depth(s):
stack = []
max_depth = 0

for char in s:
    if char == '(':
        stack.append(char)
    elif char == ')':
        if len(stack) > max_depth:
            max_depth = len(stack)
        stack.pop()

return max_depth

s = "((A+B))+(A(B-(C*D)))"
result = max_depth(s)
print("Maximum Depth:", result)

// C# code to find max depth of nested parenthesis
using System;
using System.Collections.Generic;

class Program
{
    static void Main()
    {
        string str = "((A+B))+(A(B-(C*D)))";

        int result = MaxDepth(str);

        Console.WriteLine("Maximum Depth: " + result);
    }

    public static int MaxDepth(string str)
    {
        Stack<char> st = new Stack<char>();
        int count = 0;

        foreach (char c in str)
        {
            if (c == '(')
            {
                st.Push(c);
            }
            else if (c == ')')
            {
                if (count < st.Count)
                {
                    count = st.Count;
                }
                st.Pop();
            }
        }

        return count;
    }
}

Output:

Maximum Depth: 3

• Time Complexity: O(n) where n is the size of the given input string.
• Space Complexity: O(n) as we are using an extra stack to store open parenthesis.

Maximum Depth of Nested Parenthesis Without Using Stack.

In this approach, we are not using any additional data structure like stack. If we observe the previous solution carefully then we figure out that whenever we meet a close parenthesis we are checking the current depth of the stack so we do not need to store the element in the stack. Instead, we can use a variable that will tell us the current depth, and each time we meet a closing parenthesis we will update the maximum of current and previous depth.

Algorithm steps:

• Initialize a variable depth to keep track of the current nesting depth. Initially set to 0.
• Initialize a variable ans to store the maximum depth encountered during the iteration. Initially set to 0.
• Iterate through the given string and follow the steps below:
• If the current character is opening parenthesis then increase the value of depth by 1.
• Update ans with the maximum value between its current value and the current depth.
• If the current character is a closing parenthesis ')', decrement the depth to indicate the end of nesting.
• After iterating through the entire string, return the final maximum depth stored in ans. 

Below is the code implementation of the above approach:

C++ Java Python C#

// C++ code to find the maximum depth
// of nested parenthesis without stack
#include <iostream>
#include<stack>
using namespace std;

int maxDepth(string str) {
    int depth = 0;
    int ans = 0;

    for(char c:str) {
        if(c == '(') {
            depth++;
            // update the current max depth
            ans = max(ans, depth);
        }else if(c == ')'){
            depth--;
        }
    }
    return ans;
}
int main() {
    string str = "((A+B))+(A(B-(C*D)))";

    int result = maxDepth(str);

    cout<< "Maximum Depth: " <<result <<endl;
    return 0;
}

// Java code to find the maximum depth
// of nested parenthesis without stack
public class MaxDepth {
    public static int maxDepth(String str) {
        int depth = 0;
        int ans = 0;

        for (char c : str.toCharArray()) {
            if (c == '(') {
                depth++;
                ans = Math.max(ans, depth);
            } else if (c == ')') {
                depth--;
            }
        }
        return ans;
    }

    public static void main(String[] args) {
        String str = "((A+B))+(A(B-(C*D)))";
        int result = maxDepth(str);
        System.out.println("Maximum Depth: " + result);
    }
}

# Maximum Depth of parenthesis in O(1) space
def max_depth(s):
depth = 0
ans = 0

for c in s:
    if c == '(':
        depth += 1
        ans = max(ans, depth)
    elif c == ')':
        depth -= 1

return ans

str_input = "((A+B))+(A(B-(C*D)))"
result = max_depth(str_input)
print("Maximum Depth:", result)

// C# code to find depth of nested parenthesis
using System;

class Program {
    static int MaxDepth(string str) {
        int depth = 0;
        int ans = 0;

        foreach (char c in str) {
            if (c == '(') {
                depth++;
                ans = Math.Max(ans, depth);
            } else if (c == ')') {
                depth--;
            }
        }

        return ans;
    }

    static void Main() {
        string str = "((A+B))+(A(B-(C*D)))";
        int result = MaxDepth(str);
        Console.WriteLine("Maximum Depth: " + result);
    }
}

Output:

Maximum Depth: 3

• Time Complexity: O(n) where n is the size of the input string.
• Space Complexity: O(1) as we are not using any extra space except two variables to store the current and maximum depth.

Remove Outermost Parenthesis of Primative String.

Given a string representing a valid parentheses sequence, your task is to remove the outermost parentheses of every primitive pair of parentheses. A primitive pair of parentheses is a pair that is not part of any other parentheses. Implement a function that takes a string as input and returns a modified string with the outermost parentheses removed.

• The input string s consists of parentheses characters '(' and ')' only.
• The length of s is between 1 and 1000.

Example:

Input: "(()())(())"

Output: "()()()"

Explanation: After removing the outermost parentheses of each primitive pair, the resulting string is "()()()"

Input: "((()(())))"

Output: "(()(()))"

Explanation: After removing the outermost parentheses of each primitive pair, the resulting string is "(()(()))".

There are different approaches to solving this problem of removing outermost parenthesis and here we are going to discuss two of them. Let's see each of these approaches one by one:

Remove the Outermost Parenthesis using Stack.

This approach leverages a stack data structure to keep track of opening parentheses. By iterating through the input string and using the stack to identify pairs of parentheses, the algorithm selectively removes the outermost parentheses, resulting in a modified string without those outermost pairs.

Algorithm Steps:

• Initialize an empty stack to keep track of opening parenthesis.
• Initialize an empty string (result) to store the modified string.
• Iterate through each character of the given input string:
• If the character is an opening parenthesis '(' push it onto the stack.
• If the character is closing parenthesis ')' pop from the stack and if the stack is not empty after popping then add the character to the result string.
• Return the result string. 

Below is the code implementation of the above approach:

C++ Java Python C#

// C++ code to remove outermost parenthesis 
#include <iostream>
#include <stack>
using namespace std;

//function
string removeOuterParentheses(string s) {
    stack<char> parenthesesStack;
    string result = "";

    for (char c : s) {
        if (c == '(') {
            if (!parenthesesStack.empty()) {
                result += c;
            }
            parenthesesStack.push(c);
        } else {
            parenthesesStack.pop();
            if (!parenthesesStack.empty()) {
                result += c;
            }
        }
    }

    return result;
}

int main() {
    string input = "(()())(())";
    string output = removeOuterParentheses(input);

    cout << "Original String: " << input << endl;
    cout << "Removing outermost parentheses: " << output << endl;

    return 0;
}

// Java code to remove outermost Parenthesis 
import java.util.Stack;

public class Main {
    public static void main(String[] args) {
        String input = "(()())(())";
        String output = removeOuterParentheses(input);

        System.out.println("Original String: " + input);
        System.out.println("Removing outermost parentheses: " + output);
    }

    public static String removeOuterParentheses(String s) {
        Stack<Character> parenthesesStack = new Stack<>();
        StringBuilder result = new StringBuilder();

        for (char c : s.toCharArray()) {
            if (c == '(') {
                if (!parenthesesStack.isEmpty()) {
                    result.append(c);
                }
                parenthesesStack.push(c);
            } else {
                parenthesesStack.pop();
                if (!parenthesesStack.isEmpty()) {
                    result.append(c);
                }
            }
        }

        return result.toString();
    }
}

# Python code to remove outermost parenthesis
def removeOuterParentheses(s):
parentheses_stack = []
result = ""

for c in s:
    if c == '(':
        if parentheses_stack:
            result += c
        parentheses_stack.append(c)
    else:
        parentheses_stack.pop()
        if parentheses_stack:
            result += c

return result

input_str = "(()())(())"
output_str = removeOuterParentheses(input_str)

print("Original String:", input_str)
print("Removing outermost parentheses:", output_str)

//C# code to remove outermost parenthesis
using System;
using System.Collections.Generic;

class Program
{
    static void Main()
    {
        string input = "(()())(())";
        string output = RemoveOuterParentheses(input);

        Console.WriteLine("Original String: " + input);
        Console.WriteLine("Removing outermost parentheses: " + output);
    }

    public static string RemoveOuterParentheses(string s)
    {
        Stack<char> parenthesesStack = new Stack<char>();
        System.Text.StringBuilder result = new System.Text.StringBuilder();

        foreach (char c in s)
        {
            if (c == '(')
            {
                if (parenthesesStack.Count > 0)
                {
                    result.Append(c);
                }
                parenthesesStack.Push(c);
            }
            else
            {
                parenthesesStack.Pop();
                if (parenthesesStack.Count > 0)
                {
                    result.Append(c);
                }
            }
        }

        return result.ToString();
    }
}

Output:

Original String: (()())(())
Removing outermost parentheses: ()()()

• Time Complexity: We are traversing the complete string only once so the time complexity will be O(n) where n is the length of the given input string.
• Space Complexity: We are using an extra stack to solve the problem and we are also using an extra string just to store our modified string so overall space complexity will be O(n).

Remove the Outermost Parenthesis Without Using Stack.

In this approach, the algorithm maintains a count of the depth of parentheses while iterating through the input string. By intelligently deciding which parentheses to include in the modified string based on their depth, the algorithm effectively removes the outermost parentheses of each primitive pair. This depth-counting approach provides a simple yet efficient solution to the problem.

Algorithm Steps:

• Initialize an empty string (result) to store the modified string.
• Initialize a variable (depth) to keep track of the depth of parentheses.
• Iterate through each character of the given string:
• If the character is an opening parenthesis ( and the depth is greater than 0, add it to the result.
• If the character is a closing parenthesis ) and the depth is greater than 1, add it to the result.
• Update the depth based on the current character.
• Return the result string.

Below is the code implementation of the above approach:

C++ Java Python C#

// C++ code to remove outermost parenthesis 
// without using stack 
#include <iostream>
using namespace std;

string removeOuterParentheses(string s) {
    string result = "";
    int depth = 0;

    for (char c : s) {
        if(c == '(') {
            if(depth > 0){
                result += c;
            }
            depth++;
        } else{
            depth--;
            if(depth > 0) {
                result += c;
            }
        }
    }

    return result;
}

int main() {
    string input = "(()())(())";
    string output = removeOuterParentheses(input);

    cout << "Original String: " << input << endl;
    cout << "Removing outermost parentheses: " << output << endl;

    return 0;
}

// Java code to remove Outermost Parenthesis without using stack
import java.util.Stack;

public class Main {
    public static void main(String[] args) {
        String input = "(()())(())";
        String output = removeOuterParentheses(input);

        System.out.println("Original String: " + input);
        System.out.println("Removing outermost parentheses: " + output);
    }

    public static String removeOuterParentheses(String s) {
        int depth = 0;
        StringBuilder result = new StringBuilder();

        for (char c : s.toCharArray()) {
            if (c == '(') {
                if (depth > 0) {
                    result.append(c);
                }
                depth++;
            } else {
                depth--;
                if (depth > 0) {
                    result.append(c);
                }
            }
        }

        return result.toString();
    }
}

# Python code to remove outermost parenthesis 
# without using stack
def remove_outer_parentheses(s):
    result = ""
    depth = 0

    for c in s:
        if c == '(':
            if depth > 0:
                result += c
            depth += 1
        else:
            depth -= 1
            if depth > 0:
                result += c

    return result

# Example usage
input_str = "(()())(())"
output_str = remove_outer_parentheses(input_str)

print("Original String:", input_str)
print("Removing outermost parentheses:", output_str)

// C# code implementation to remove 
// outermost parenthesis without using stack
using System;

class Program
{
    static void Main()
    {
        string input = "(()())(())";
        string output = RemoveOuterParentheses(input);

        Console.WriteLine("Original String: " + input);
        Console.WriteLine("Removing outermost parentheses: " + output);
    }

    public static string RemoveOuterParentheses(string s)
    {
        string result = "";
        int depth = 0;

        foreach (char c in s)
        {
            if (c == '(')
            {
                if (depth > 0)
                {
                    result += c;
                }
                depth++;
            }
            else
            {
                depth--;
                if (depth > 0)
                {
                    result += c;
                }
            }
        }

        return result;
    }
}

Output:

Original String: (()())(())
Removing outermost parentheses: ()()()

• Time Complexity: We are traversing the given input string only once so the time complexity will be O(n) where n is the length of the given string.
• Space Complexity: We are not using any extra space except the result string which we are using only to store our answer so the overall space complexity is O(1).

Check Balanced Parenthesis in an Expression.

Given an expression containing various types of parentheses ((), {}, []), you need to determine if the parentheses are balanced. An expression is considered balanced if every opening parenthesis has a corresponding closing parenthesis and they occur in the correct order.

Example:

Input: ({[]})

Output: true

Explanation: All pairs of parenthesis are balanced.

Input: ())(

Output: false

Explanation: All pairs of parenthesis are not balanced.

Input: [(){}]

Output: true

There are different ways to solve this problem and here we are going to discuss two of them:

Check Valid Balanced Parenthesis Using Stack.

In this approach, we use a stack data structure to solve this problem of checking balance parenthesis. It is because by nature parenthesis must occur in pairs and in the correct order and the stack LIFO property is best to handle such patterns.

Algorithm Steps to Validate Parenthesis:

Step 1: Initialize an empty stack to hold the opening parenthesis.

Step 2: Iterate through each character of the expression:

• If the character is an opening parenthesis ('(', '{', '['), push it onto the stack.
• If the character is a closing parenthesis (')', '}', ']') then check if the stack is empty then return false (unbalanced) else pop the top element and check if it matches with the closing parenthesis.
• If the closing parenthesis does not match with the top element of the stack then return false.

Step 3: After iteration, check if the stack is empty (balanced) and return true, else return false (unbalanced).

Example Illustration.

Below is the code implementation of the above approach:

C++ Java Python C#

// C++ code implementation to check balanced parenthesis
#include<iostream>
#include<stack>
using namespace std;

//function to check balance parenthesis
bool validParenthesis(string str){
    stack<char> st;

    for(int i = 0; i < str.size(); i++){
        //opening parenthesis, push into the stack
        if(str[i] == '{' || str[i] == '[' || str[i] == '(') {
            st.push(str[i]);    
        }else if(str[i] == '}' || str[i] == ']' || str[i] == ')') {
            
            //empty stack
            if(st.empty())
               return false;
            
            //check if stack top contain a matching opening bracket
            //pop the top element if matching is found
            if((st.top() == '{' && str[i] == '}') 
            || (st.top() == '[' && str[i] == ']') 
            || (st.top() == '(' && str[i] == ')')) {
                st.pop();
            }
            else{
                return false;
            } 
        }
    }
    //stack is empty after complete iteration
    if(st.empty()) 
       return true;
    
    return false;   
}
int main() {
    string str = "[{(){()}}]";

    if(validParenthesis(str)){
        cout<<"Balance Parenthesis"<<endl;
    }else{
        cout<<"Unbalance Parenthesis"<<endl;
    }
    return 0;
}

// Java Code Implementation to check balanced parenthesis
import java.util.Stack;

public class ParenthesisChecker {
    public static boolean isValidParenthesis(String str) {
        Stack<Character> stack = new Stack<>();
        //push the char in stack if they are opening brackets
        for (char ch : str.toCharArray()) {
            if (ch == '{' || ch == '[' || ch == '(') {
                stack.push(ch);
            } else if (ch == '}' || ch == ']' || ch == ')') {
                if (stack.isEmpty()) return false;
                
             
              //pop the top element if matching bracket is found
                char top = stack.pop();
                if ((top == '{' && ch == '}') || (top == '[' && ch == ']') 
                || (top == '(' && ch == ')')) {
                    continue;
                } else {
                    return false; // Mismatched brackets
                }
            }
        }

        return stack.isEmpty();
    }

    public static void main(String[] args) {
        String str = "[{(){()}}]";

        if (isValidParenthesis(str)) {
            System.out.println("Balanced Parenthesis");
        } else {
            System.out.println("Unbalanced Parenthesis");
        }
    }
}

# Python code to check balanced parenthesis
def is_valid_parenthesis(s):
stack = []

for char in s:
    # checking for open brackets
    if char in '{[(':
        stack.append(char)
    # checking for closing brackets    
    elif char in '})]':
        if not stack:
            return False
        
        # pop the top char from stack if matching pair is found
        top = stack.pop()
        if (top == '{' and char == '}') or (top == '[' and char == ']') or (top == '(' and char == ')'):
            pass
        else:
            return False  # Mismatched brackets

return not stack


# Example usage
parenthesis_str = "[{(){()}}]"
if is_valid_parenthesis(parenthesis_str):
print("Balanced Parenthesis")
else:
print("Unbalanced Parenthesis")

// C# code to check balanced parenthesis
using System;
using System.Collections.Generic;

class ParenthesisChecker
{
    static bool IsValidParenthesis(string str)
    {
        Stack<char> stack = new Stack<char>();

        foreach (char ch in str)
        {   // push the char in stack if it is opening bracket
            if (ch == '{' || ch == '[' || ch == '(')
            {
                stack.Push(ch);
            }
            // pop the top char from stack if it is matching pair of closing bracket 
            else if (ch == '}' || ch == ']' || ch == ')')
            {
                if (stack.Count == 0) return false;

                char top = stack.Pop();
                if ((top == '{' && ch == '}') || (top == '[' && ch == ']') 
                  || (top == '(' && ch == ')'))
                {
                    continue;// Matching brackets, continue
                }
                else
                {
                    return false; // Mismatched brackets
                }
            }
        }

        return stack.Count == 0;
    }

    static void Main()
    {
        string str = "[{(){()}}]";

        if (IsValidParenthesis(str))
        {
            Console.WriteLine("Balanced Parenthesis");
        }
        else
        {
            Console.WriteLine("Unbalanced Parenthesis");
        }
    }
}

Output:

Balanced Parenthesis

• Time Complexity: The algorithm iterates through each character in the expression once, resulting in a time complexity of O(n), where n is the length of the expression.
• Space Complexity: The space complexity is O(n), where n is the length of the expression. This is due to the stack storing opening parentheses, and in the worst case, the stack may contain all opening parentheses before encountering the corresponding closing ones.

Check Balanced Parenthesis Without Using Stack.

While the stack is a convenient data structure for checking balanced parentheses, it's possible to achieve the same goal without using a stack. 

Algorithm Steps:

Step 1: Initialize an integer variable i to -1. This variable will be used to track the top of the stack.

Step 2: Iterate through the expression:

• If ch is an opening parenthesis ('(', '{', '[') then increase the value of i by 1 and replace the character at index i in the expression with the opening bracket.
• If ch is a closing parenthesis (')', '}', ']') check if i is greater than or equal to 0. Check if the current closing bracket matches the corresponding opening bracket at index i: If yes, decrement i by 1 else returns false.

Step 3: After completing the iteration check if i is equal to -1 return true else return false.

Below is the code implementation of the above approach:

C++ Java Python C#

// C++ code to check balance parenthesis without stack
#include<iostream>
using namespace std;

//function to check parenthesis is balance or not
bool validParenthesis(string str) {
    // Initialize an index variable for tracking the top of the stack
    int i = -1;

    for(int j  = 0; j < str.size(); j++) {

        if(str[j] == '{' || str[j] == '[' || str[j] == '('){

           // Increment counter for opening parenthesis 
           i++;

           // Replace ith character with the opening bracket
           str[i] = str[j];
        }
        else{
          if(i >= 0 && ((str[i] == '(' && str[j] == ')') 
                     || (str[i] == '{' && str[j] == '}') 
                     || (str[i] == '[' && str[j] == ']'))) {
            // Decrement counter for matching closing parenthesis
            i--;
          }
          else {
            return false;
          }
        }
    }
    // -1 indicate that stack is empty (balanced parenthesis)
    if(i == -1) return true;
    
    return false;
}
int main() {
    string str = "({[][{]})";

    if(validParenthesis(str)){
        cout<<"Balance Parenthesis"<<endl;
    }else{
        cout<<"Unbalance Parenthesis"<<endl;
    }
    return 0;
}

// Java code implementation to check valid parenthesis
import java.util.Scanner;

public class Main {
    // Function to check if parentheses are balanced
    static boolean validParenthesis(String str) {
        StringBuilder sb = new StringBuilder();
        int i = -1;

        for (int j = 0; j < str.length(); j++) {
            char ch = str.charAt(j);

            if (ch == '{' || ch == '[' || ch == '(') {
                i++;
                sb.append(ch);
            } else {
                if (i >= 0 && ((sb.charAt(i) == '(' && ch == ')') || 

                   (sb.charAt(i) == '{' && ch == '}') || (sb.charAt(i) == '[' && ch == ']'))) {
                    i--;
                } else {
                    return false;
                }
            }
        }
        return i == -1;
    }

    public static void main(String[] args) {
        String str = "({[][{]})";

        if (validParenthesis(str)) {
            System.out.println("Balanced Parenthesis");
        } else {
            System.out.println("Unbalanced Parenthesis");
        }
    }
}

# Python program to validate parenthesis
def validParenthesis(s):
i = -1

for j in range(len(s)):
    if s[j] in ['{', '[', '(']:
        i += 1
        s = s[:i + 1] + s[j]
    else:
        if i >= 0 and ((s[i] == '(' and s[j] == ')') or (s[i] == '{' and s[j] == '}') or (s[i] == '[' and s[j] == ']')):
            i -= 1
        else:
            return False

return i == -1

str_value = "({[][{]})"
if validParenthesis(str_value):
print("Balanced Parenthesis")
else:
print("Unbalanced Parenthesis")

// C# code to check valid balanced parenthesis
using System;

class Program
{
    // Function to check if parentheses are balanced
    static bool ValidParenthesis(string str)
    {
        int i = -1;
        char[] sb = new char[str.Length];
        for (int j = 0; j < str.Length; j++)
        {
            char ch = str[j];

            if (ch == '{' || ch == '[' || ch == '(')
            {
                i++;
                sb[i] = ch;
            }
            else
            {
                if (i >= 0 && ((sb[i] == '(' && ch == ')') || (sb[i] == '{' && ch == '}') 

                   || (sb[i] == '[' && ch == ']')))
                {
                    i--;
                }
                else
                {
                    return false;
                }
            }
        }
        return i == -1;
    }

    static void Main()
    {
        string str = "({[][]})";

        if (ValidParenthesis(str))
        {
            Console.WriteLine("Balanced Parenthesis");
        }
        else
        {
            Console.WriteLine("Unbalanced Parenthesis");
        }
    }
}

Output:

Unbalanced Parenthesis

• Time Complexity: Time complexity of the above solution in O(n) where n is the length of the given expression.
• Space Complexity: Space complexity is O(1) if it is allowed to modify the existing string otherwise, it will be O(n).