Merge Two Sorted Linked List in C++.

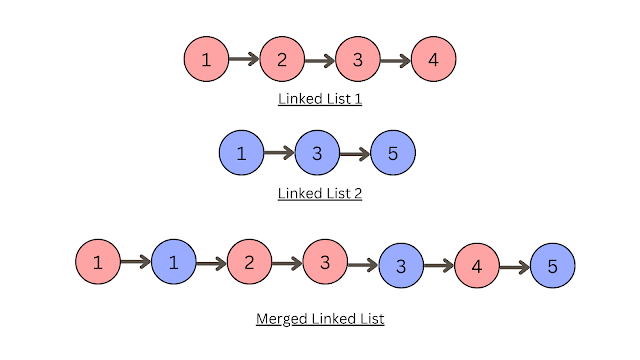
Given heads of two sorted Linked lists list1 and list2 arrange in ascending order. Merge the two linked lists into one sorted linked list and return the head of the merged list.

Example 1: 
Input: 

list1: 1->2->3->4->NULL

list2: 1->3->5->NULL
Output: 1->1->2->3->3->4->5->NULL

Example 2:
Input: 

list1: 1->NULL
list2: 
Output: 1->NULL

Approach 1: Brute Force (Using Iteration). 

Follow the below steps to merge two sorted linked lists:

• If list1 is NULL then simply return the head of list2 and if list2 is NULL then simply return the head of list1.
• Declare a temp pointer that will point to a list containing the smaller value in the head node.
• One traverses the lists until one of them gets exhausted, chooses a smaller current node and links it with the tail of the merged list and then moves the current pointer of that list one step forward.
• If you reach a condition in which one of the lists got exhausted then simply link the remaining list to the tail of the merged list.

C++ Solution code:

/*C++ Program to Merge Sorted Linked List*/
#include<bits/stdc++.h>
using namespace std;

class ListNode{
    public:
      int data;
      ListNode *next;

    //constructor
    ListNode(int data){
        this->data = data;
        this->next = NULL;
    }  
};
//creating new node
ListNode *newNode(int data){
    ListNode *temp = new ListNode(data);
    temp->next = NULL;
    return temp;
}
//function to merge sorted linked lists
ListNode *mergeList(ListNode *list1, ListNode *list2){

    if(list1 == NULL ) return list2;
    if(list2 == NULL ) return list2;

    ListNode *ptr;
    if(list1->data > list2->data){
        ptr = list2;
        list2 = list2->next;
    }
    else{
        ptr = list1;
        list1 = list1->next;
    }

    ListNode *curr = ptr;

    while(list1 != NULL && list2 != NULL){

        if(list1->data < list2->data){
            curr->next = list1;
            list1 = list1->next;
        }
        else{
            curr->next = list2;
            list2 = list2->next;
        }
        curr = curr->next;
    }
    if(list1 != NULL){
        curr->next = list1;
    }
    else{
        curr->next = list2;
    }
    return ptr;
}
//function to print linked list
void printList(ListNode *head){
    ListNode *temp = head;

    while(temp != NULL){
        cout<<temp->data<<" ";
        temp = temp->next;
    }
}
int main(){
    //sorted list 1
    ListNode *list1 = newNode(1);
    list1->next = newNode(2);
    list1->next->next = newNode(3);
    list1->next->next->next = newNode(4);
    //sorted list 2
    ListNode *list2 = newNode(1);
    list2->next = newNode(3);
    list2->next->next = newNode(5);

    ListNode *merge = NULL;

    cout<<"Linked List1: ";
    printList(list1);

    cout<<"\nLinked List2: ";
    printList(list2);

    merge = mergeList(list1, list2);

    cout<<"\nSorted Linked List after merge: ";
    printList(merge);
    return 0;
}

Output:

Linked List1: 1 2 3 4
Linked List2: 1 3 5
Sorted Linked List after merge: 1 1 2 3 3 4 5

• Time Complexity: O(n) where n is the total number of nodes by adding list1 and list2.
• Space Complexity: O(1) no extra space is required.

Related Articles:

• Convert Binary Linked List to Integer.

• Find the Middle of the Singly Linked List in C++.

• Reverse a Singly Linked List in C++.

• Intersection Point of Two Linked Lists in C++.

• Detect Cycle in a Linked List in C++.

Reverse a Singly Linked List in C++.

Given the head of the singly linked list, reverse the given linked list and return it. 

Example 1: 
Input: 1->2->3->4->5->NULL
Output: 5->4->3->2->1->NULL

Example 2:
Input: 1->0->4->7->2->3->NULL
Output: 3->2->7->4->0->1->NULL

Approach 1: Using Three Pointer.

In this approach, you need a three-pointer previous(prev), current(curr), and next(nxt) to keep track of nodes. 

Initialize three-pointers, prev as NULL, curr as head of the linked list and next as NULL.

Iterate through the linked list and follow below four steps to reverse the linked list:

• next = curr->next;
• curr->next = prev;
• prev = curr;
• curr = next;

C++ Solution code:

/*C++ Program to reverse a linked list*/
#include<bits/stdc++.h>
using namespace std;

class ListNode{
    public:
      int data;
      ListNode *next;

    //constructor
    ListNode(int data){
        this->data = data;
        this->next = NULL;
    }  
};
//creating new node
ListNode *newNode(int data){
    ListNode *temp = new ListNode(data);
    temp->next = NULL;
    return temp;
}
//function to reverse linked list
ListNode *reverseList(ListNode *head){

    ListNode *curr = head;
    ListNode *prev = NULL, *next = NULL;

    while(curr != NULL){
        next = curr->next;
        curr->next = prev;
        prev = curr;
        curr = next;
    }
    head = prev;
    return head;
}
//function to print linked list
void printList(ListNode *head){
    ListNode *temp = head;

    while(temp != NULL){
        cout<<temp->data<<" ";
        temp = temp->next;
    }
}
int main(){
    ListNode *head = newNode(1);
    head->next = newNode(2);
    head->next->next = newNode(3);
    head->next->next->next = newNode(4);
    head->next->next->next->next = newNode(5);

    cout<<"Linked List before reverse: ";
    printList(head);

    ListNode *newHead = reverseList(head);

    cout<<"\nLinked List after reverse: ";
    printList(newHead);
    return 0;
}

Output:

Linked List before reverse: 1 2 3 4 5
Linked List after reverse: 5 4 3 2 1

• Time Complexity: O(n)
• Space Complexity: O(1)

Approach 2: Using Recursion.

This is a baisc recurison in which one base is when head is NULL or head->next is NULL. It means our list contain no node or it contain only one node and we cannot reverse a single node.

C++ Solution Code:

/*C++ Program to reverse a linked list using recursion*/
#include<bits/stdc++.h>
using namespace std;

class ListNode{
    public:
      int data;
      ListNode *next;

    //constructor
    ListNode(int data){
        this->data = data;
        this->next = NULL;
    }  
};
//creating new node
ListNode *newNode(int data){
    ListNode *temp = new ListNode(data);
    temp->next = NULL;
    return temp;
}
//function to reverse linked list
ListNode *reverseList(ListNode *head){

    //base case
    if(head == NULL || head->next == NULL)
       return head;

    ListNode *newHead = reverseList(head->next);
    head->next->next = head;

    head->next = NULL;

    return newHead;
}
//function to print linked list
void printList(ListNode *head){
    ListNode *temp = head;

    while(temp != NULL){
        cout<<temp->data<<" ";
        temp = temp->next;
    }
}
int main(){
    ListNode *head = newNode(1);
    head->next = newNode(2);
    head->next->next = newNode(3);
    head->next->next->next = newNode(4);
    head->next->next->next->next = newNode(5);

    cout<<"Linked List before reverse: ";
    printList(head);

    ListNode *newHead = reverseList(head);

    cout<<"\nLinked List after reverse: ";
    printList(newHead);
    return 0;
}

Output:

Linked List before reverse: 1 2 3 4 5
Linked List after reverse: 5 4 3 2 1

• Time Complexity: O(n)
• Space Complexity: O(n) stack space

Related Articles:

• Convert Binary Linked List to Integer.

• Find the Middle of the Singly Linked List in C++.

• Merge Two Sorted Linked List in C++.

• Intersection Point of Two Linked Lists in C++.

• Detect Cycle in a Linked List in C++.

Find Middle of the Singly Linked List in C++.

Given a singly linked list and you need to return the middle node of the list and if the list has two middle nodes then return the second middle node.

Example 1: 
Input: 1->2->3->4->5
Output: 3

Example 2:
Input: 1->0->4->7->2->3
Output: 7

This problem is very simple to solve we just need to find the length of the linked list and then divide the length by 2 to get the indexing middle node. There are multiple ways to solve the problem let's discuss them one by one.

Approach 1: Brute Force Approach.

• Traverse the whole linked list to find the length of the linked list.
• Calculate the position of the middle node by diving the length of the linked list by 2. (len/2)
• After getting the position of the middle node traverse the linked list again using the temp pointer to find the address of the middle node.

C++ Solution Code:

/*C++ Program to find the middle element of the linked list*/
#include<bits/stdc++.h>
using namespace std;

class ListNode{
    public:
      int data;
      ListNode *next;

    //constructor
    ListNode(int data){
        this->data = data;
        this->next = NULL;
    }  
};
//creating new node
ListNode *newNode(int data){
    ListNode *temp = new ListNode(data);
    temp->next = NULL;
    return temp;
}
//Length of linked list
int getLength(ListNode *head){
    int len = 0;
    ListNode *temp = head;
    while(temp != NULL){
        temp = temp->next;
        len++;
    }
    return len;
}
//Function to get middle element
int getMiddle(ListNode* head){

    int len = getLength(head);

    ListNode *temp = head;
    int middle = len/2;

    while(middle--){
        temp = temp->next;
    }
    return temp->data;
}

int main(){
    ListNode *head = newNode(1);
    head->next = newNode(2);
    head->next->next = newNode(3);
    head->next->next->next = newNode(4);
    head->next->next->next->next = newNode(5);

    cout<<"Middle Element: "<<getMiddle(head);

    return 0;
}

Output:

Middle Element: 3

• Time Complexity: O(n) + O(n/2) = O(n)
• Space Complexity: O(1)

Approach 2: Two-pointer approach (Slow Fast Pointer).

The second method is known as the Tortoise and Hare method or slow and fast pointer approach. In this approach, one pointer moves faster than the other pointer, and by the time the faster pointer reaches the end of the linked list, the slower point will reach the middle of the list. 

Step 1

Step 2

Step 3

• Initialize two pointers, slow and fast with the head of the linked list.
• Every time the slow moves one step the fast pointer move two-step at the same time.
• When the fast pointer reaches the end, you need to return the value present at the slow pointer which is pointing to the middle of the list.

C++ Solution code:

/*C++ Program to find the middle element of the linked list
using slow and fast pointer approach*/
#include<bits/stdc++.h>
using namespace std;

class ListNode{
    public:
      int data;
      ListNode *next;

    //constructor
    ListNode(int data){
        this->data = data;
        this->next = NULL;
    }  
};
//creating new node
ListNode *newNode(int data){
    ListNode *temp = new ListNode(data);
    temp->next = NULL;
    return temp;
}

//Function to get middle element
int getMiddle(ListNode* head){

    ListNode *slow = head;
    ListNode *fast = head;

    while(fast && fast->next){
        slow = slow->next;
        fast = fast->next->next;
    }
    return slow->data;
}

int main(){
    ListNode *head = newNode(1);
    head->next = newNode(2);
    head->next->next = newNode(3);
    head->next->next->next = newNode(4);
    head->next->next->next->next = newNode(5);

    cout<<"Middle Element: "<<getMiddle(head);

    return 0;
}

Output:

Middle Element: 3

• Time Complexity: O(n/2) = O(n)
• Space Complexity: O(1)

Related Articles:

• Convert Binary Linked List to Integer.

• Reverse a Singly Linked List in C++.

• Merge Two Sorted Linked List in C++.

• Intersection Point of Two Linked Lists in C++.

• Detect Cycle in a Linked List in C++.

Convert Binary Linked List to Integer.

Given a Singly Linked List containing n nodes, each node of the list can hold either 0 or 1 and the most significant bit is present at the head of the linked list. The entire linked list is a binary representation of a decimal number. Return the decimal value represented by the given binary linked list. 

Note: The linked list is not empty and the maximum number of nodes will be less than 30.

Example 1: 
Input: 1->0->1->1
Output: 11

Example 2:
Input: 1->0->1
Output: 5

Approach 1: Converting Binary Using Arithmetic calculation.

You can solve this problem by diving the problem into two sub-problems:

• Find the number of binary digits present in the given linked list that is needed for the arithmetic calculation.
• Convert the Binary to a Decimal number using classic arithmetic calculation (see the above image).

C++ Solution Code:

//C++ Program to convert Binary Linked List to Decimal
#include<bits/stdc++.h>
using namespace std;

class ListNode{
    public:
      int data;
      ListNode *next;

    //constructor
    ListNode(int data){
        this->data = data;
        this->next = NULL;
    }  
};
//creating new node
ListNode *newNode(int data){
    ListNode *temp = new ListNode(data);
    temp->next = NULL;
    return temp;
}
//function to find length of linked list
int listLength(ListNode* head){
    ListNode *temp = head;
    int len = 0;
    while(temp != NULL){
        temp = temp->next;
        len++;
    }
    return len;
}
//function to convert binary to decimal
int getDecimalValue(ListNode *head){
    
    int len = listLength(head);
    int ans = 0;
    ListNode *temp = head;
    int i = 1;

    while(temp != NULL){
        int res = (temp->data)*pow(2, len-i);
        temp = temp->next;
        i++;
        ans += res;
    }
    return ans;
}
int main(){
    ListNode *head = newNode(1);
    head->next = newNode(0);
    head->next->next = newNode(1);

    cout<<"Integer Value: "<<getDecimalValue(head);

    return 0;
}

Output:

Integer Value: 5

• Time Complexity: O(n)
• Space Complexity: O(1)

Approach 2: Using Bit Manipulation.

In this approach, bit manipulation technique in which we will traverse the linked list starting from head till end. Updating the current value with head->next->value. Updating the result by shifting the digit by one to the left and performing logical OR with current vlaue.

C++ Solution code:

/*C++ Program to convert Binary Linked List to Decimal
Using bit manipulation*/
#include<bits/stdc++.h>
using namespace std;

class ListNode{
    public:
      int data;
      ListNode *next;

    //constructor
    ListNode(int data){
        this->data = data;
        this->next = NULL;
    }  
};
//creating new node
ListNode *newNode(int data){
    ListNode *temp = new ListNode(data);
    temp->next = NULL;
    return temp;
}

//function to convert binary to decimal
int getDecimalValue(ListNode *head){
    
    int num = head->data;
    while (head->next != NULL)
    {
        num = (num << 1) | head->next->data;
        head = head->next;
    }
    
    return num;
}
int main(){
    ListNode *head = newNode(1);
    head->next = newNode(0);
    head->next->next = newNode(1);

    cout<<"Integer Value: "<<getDecimalValue(head);

    return 0;
}

Output:

Integer Value: 5

• Time Complexity: O(n)
• Space Complexity: O(1)

Related Articles:

• Find the Middle of the Singly Linked List in C++.

• Reverse a Singly Linked List in C++.

• Merge Two Sorted Linked List in C++.

• Intersection Point of Two Linked Lists in C++.

• Detect Cycle in a Linked List in C++.

Program to Find Sum of All Odd Length Subarrays.

Given a positive integer array num of size n, calculate and return the sum of all possible odd-length subarrays of num.

Example:

Example 1:
Input: num[] = {1, 3, 2, 5, 6};
Output: 63

Explanation: 
List of Odd length subarrays:

[1] = 1

[3] = 3

[2] = 2

[5] = 5

[6] = 6

[1, 3, 2] = 6

[3, 2, 5] = 10

[2, 5, 6] = 13

[1, 3, 2, 5, 6] = 17

Sum of all odd length arrays: 1+3+2+5+6+6+10+13+17 = 63

Example 2:
Input: num[] = {3, 5}
Output: 8

Explanation:

List of Odd length subarrays:

[3] = 3

[5] = 5

Sum of all odd length arrays: 3+5 = 8

Approach 1: Brute Force Solution.

You can quickly get all possible subarrays by running two nested loops but the critical point of this problem is that you need to find only all odd-length subarrays. 

You can use a generalized formula that if [(last_position_of_subarray - first_positon_ of _subarray)%2 == 0] then the length is odd else the length is even. You can then add the elements of that subarray to your answer.

C++ Solution Code:

/*C++ code to find sum of odd length subarray*/
#include<bits/stdc++.h>
using namespace std;

int sumOfOddSubarray(vector<int> &num){
    int total = 0;

    for(int i = 0; i < num.size(); i++){
        int sum = 0;
        for(int j = i; j < num.size(); j++){
            sum += num[j];
            if((j - i)%2 == 0)
              total += sum;
        }
    }
    return total;
}

int main(){
    vector<int> num = {1, 3, 2, 5, 6};

    int ans = sumOfOddSubarray(num);
    cout<<"Sum Of Odd Length subarrays: "<<ans;

    return 0;   
}

Output:

Sum Of Odd Length subarrays: 63

• Time Complexity: O(n^2)
• Space Complexity: O(1)

Approach 2: Using Math.

In the previous approach, you check for all possible subarrays but in this approach, you are going to derive a mathematical formula to solve this problem in O(n) time complexity. This solution might be a little confusing but if you don't give up I am sure you will understand it well. Let's start,

If you observe the question carefully you will find that we only need the sum of subarrays we don't need to print them anywhere so if somehow you count the number of occurrences of each element in all possible odd-length subarray then you can multiply each element with their number of occurrences and sum them up together then you can get your required answer. Let's understand with one example.

In this above example image, we have taken only all odd-length subarrays 

Given: [1, 4, 2, 5, 3]

Element      Number of occurance      Sum

ar[0] = 1        3                    1x3 = 3

ar[1] = 4        4                    4x4 = 16

ar[2] = 2        5                    2x5 = 10

ar[3] = 5        4                    5x4 = 20

ar[4] = 3        3                    3x3 = 9

                                    Total = 58

Explanation: 

arr[2] = 2 present in 5 times(one time in row first, 

three times in row second and one time in row third)

similarly we need to count for all elements.

To create a subarray that contains arr[i]  we can take 0, 1, 2, ..... i element on the left hand side from arr[0] to  arr[i] and you get (i+1) choices to include arr[i] in the subarray. Similarly, you can take 0, 1, 2, ...... n-1-i element on the right-hand side from arr[i] to arr[n-1]. and you will get (n-i) choices to include arr[i] in the subarray.

In total you will get [k = (i+1)*(n-i)] number of subarrays that contains arr[i] so,

There is (k+1)/2 subarray with the odd length that contains arr[i].

There is (k/2) subarray with even length that contains arr[i].

We can derive a general formula with all the above observations and calculations for finding the number of times an element is occurring for odd-length subarrays.

n = ((i+1)*(n-i)+1)/2

C++ Solution Code:

/*C++ code to find sum of odd length subarray (Optimized)*/
#include<bits/stdc++.h>
using namespace std;

int sumOfOddSubarray(vector<int> &num){
    int total = 0;
    int n = num.size();

    for(int i = 0; i < n; i++){
        total += ((i+1)*(n-i)+1)/2 * num[i];
    }
    return total;
}

int main(){
    vector<int> num = {1, 4, 2, 5, 3};

    int ans = sumOfOddSubarray(num);
    cout<<"Sum Of Odd Length subarrays: "<<ans;

    return 0;   
}

Output:

Sum Of Odd Length subarrays: 58

• Time Complexity: O(n)
• Space Complexity: O(1)