Monotonic Stack.

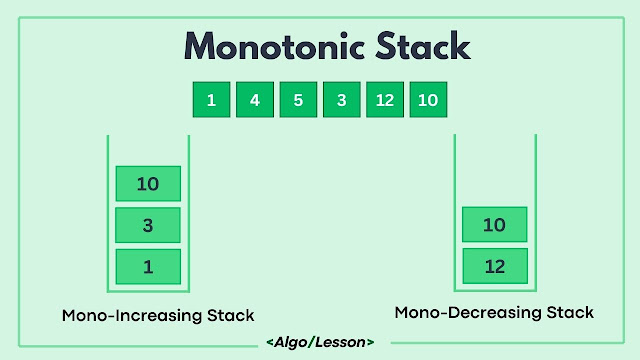
A monotonic stack is a stack-based data structure used in solving problems related to finding the next greater or smaller element, computing the nearest or farthest smaller or larger elements, or solving various range-based problems efficiently. It maintains a certain monotonic property, either non-increasing or non-decreasing while traversing through elements in the stack.

Note: In mathematics, "monotonic refers to the behavior or trend of a function or sequence that consistently moves in one direction without reversing or fluctuating. 

What is a Monotonic Stack?

The primary purpose of a monotonic stack is to facilitate efficient queries for elements that satisfy certain conditions within a sequence or an array. It allows constant-time access to specific elements by leveraging its monotonic property, making it ideal for scenarios where the order of elements is crucial.

A monotonic stack can either be non-increasing or non-decreasing. A non-increasing monotonic stack maintains elements in decreasing order from the stack's base to its top. Conversely, a non-decreasing monotonic stack arranges elements in increasing order within the stack.

Key features of Monotonic stack:

• A normal stack but its elements are in monotonically decreasing/increasing order. 

• The next element can only be pushed if it maintains the order. 

• If pushing the next element violates the order, pop elements until it can be safely pushed.

Types of Monotonic Stack.

Monotonic stacks can be categorized into two types based on the order they maintain.

• Non-Increasing monotonic stack.
• Non-decreasing monotonic stack.

Non-increasing Monotonic stack.

This stack type maintains elements in decreasing order from the base to the top of the stack. To push an element onto the stack, elements greater than the incoming element are removed (popped) to sustain the decreasing order. 

Example:

Consider the input array [5, 3, 9, 6, 2, 8]

Step-by-step process:

• Initially, the stack is empty.

• Push 5 onto the stack: Stack contains [5].

• Push 3 onto the stack: Stack contains [5, 3].

• Push 9 onto the stack: Since 9 is greater than 5 and 3, we remove 5 and 3 and the stack becomes [9].

• Push 6 onto the stack: Stack contains [9, 6].

• Push 2 onto the stack: Stack contains [9, 6, 2].

• Push 8 onto the stack: Since 8 is greater than 6 and 2, we remove 6 and 2 and the stack becomes [9, 8].

• After processing all the elements, the resultant stack is [9, 8].

Code Implementation:

Below is the code implementation of the Non-Increasing Monotonic Stack:

C++ Java Python C#

#include <iostream>
#include <stack>
#include <vector>

using namespace std;

// Function to find a monotonic decreasing stack
vector<int> decreasingStack(const vector<int>& arr) {
    stack<int> stk;
    vector<int> result;

    for (int num : arr) {
        while (!stk.empty() && stk.top() < num) {
            stk.pop();
        }
        stk.push(num);
    }

    int n = stk.size();
    result.resize(n);
    int i = n - 1;

    // Empty stack
    while (!stk.empty()) {
        result[i--] = stk.top();
        stk.pop();
    }

    return result;
}

// Driver code
int main() {
    vector<int> arr = {12, 17, 11, 13, 14, 10};

    // Function Call
    vector<int> result = decreasingStack(arr);

    // Displaying the original array
    cout << "The Original Array: ";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;

    // Displaying Monotonic Decreasing Stack
    cout << "The Monotonic Stack: ";
    for (int num : result) {
        cout << num << " ";
    }
    cout << endl;

    return 0;
}

import java.util.Stack;

public class MonotonicDecreasingStack {

  // Function to find a monotonic decreasing stack
  static int[] decreasingStack(int[] arr) {
      Stack<Integer> stack = new Stack<>();
      
      for (int num : arr) {
          while (!stack.isEmpty() && stack.peek() < num) {
              stack.pop();
          }
          stack.push(num);
      }

      int n = stack.size();
      int[] result = new int[n];
      int i = n - 1;

      // Empty stack
      while (!stack.isEmpty()) {
          result[i--] = stack.pop();
      }

      return result;
  }

  // Driver code
  public static void main(String[] args) {
      int[] arr = {12, 17, 11, 13, 14, 10};

      // Function Call
      int[] result = decreasingStack(arr);

      // Displaying the original array
      System.out.print("The Original Array: ");
      for (int num : arr) {
          System.out.print(num + " ");
      }
      System.out.println();

      // Displaying Monotonic Decreasing Stack
      System.out.print("The Monotonic Stack: ");
      for (int num : result) {
          System.out.print(num + " ");
      }
      System.out.println();
  }
}

def decreasing_stack(arr):
    stack = []
    result = []

    for num in arr:
        while stack and stack[-1] < num:
            stack.pop()
        stack.append(num)

    # Empty stack
    while stack:
        result.insert(0, stack.pop())

    return result

# Driver code
arr = [12, 17, 11, 13, 14, 10]

# Function Call
result = decreasing_stack(arr)

# Displaying the original array
print("The Original Array:", *arr)

# Displaying Monotonic Decreasing Stack
print("The Monotonic Stack:", *result)

using System;
using System.Collections.Generic;

class Program
{
    // Function to find a monotonic decreasing stack
    static int[] DecreasingStack(int[] arr)
    {
        Stack<int> stack = new Stack<int>();

        foreach (int num in arr)
        {
            while (stack.Count > 0 && stack.Peek() < num)
            {
                stack.Pop();
            }
            stack.Push(num);
        }

        int n = stack.Count;
        int[] result = new int[n];
        int i = n - 1;

        // Empty stack
        while (stack.Count > 0)
        {
            result[i--] = stack.Pop();
        }

        return result;
    }

    // Driver code
    static void Main()
    {
        int[] arr = { 12, 17, 11, 13, 14, 10 };

        // Function Call
        int[] result = DecreasingStack(arr);

        // Displaying the original array
        Console.Write("The Original Array: ");
        foreach (int num in arr)
        {
            Console.Write(num + " ");
        }
        Console.WriteLine();

        // Displaying Monotonic Decreasing Stack
        Console.Write("The Monotonic Stack: ");
        foreach (int num in result)
        {
            Console.Write(num + " ");
        }
        Console.WriteLine();
    }
}

Output:

The Original Array: 12 17 11 13 14 10 
The Monotonic Stack: 17 14 10

Time Complexity: The time complexity of the code is O(N), where N is the number of elements in the input array. This is because the code iterates through each element of the array exactly once.

Space Complexity: The space complexity is also O(N), where N is the number of elements in the input array. The space is used for the stack and the result array.

Non-Decreasing Monotonic Stack.

This stack type maintains elements in increasing order from the base to the top of the stack. When we want to push an element onto the stack, elements smaller than the incoming element are removed (popped) to maintain the increasing order.

Example:

Consider the input array [4, 7, 2, 9, 5, 1]

• Initially, the stack is empty.

• Push 4 onto the stack: Stack contains[4].

• Push 7 onto the stack: Stack contains[4, 7].

• Push 2 onto the stack: Since 2 is smaller than 7 and 4, we remove 7 and 4 and push 2. [2].

• Push 9 onto the stack: Stack contains[2, 9].

• Push 5 onto the stack: Since 5 is smaller than 9, we remove 9 and push 5. [2, 5].

• Push 1 onto the stack: Since 1 is smaller than 2 and 5, we remove 2 and 5 and push 1 [1].

• After processing all elements, the resultant stack is [1].

Code Implementation:

Below is the code implementation of the Non-Decreasing Monotonic Stack:

C++ Java Python C#

#include <iostream>
#include <stack>
#include <vector>

using namespace std;

// Function to build a monotonic increasing stack
vector<int> increasingStack(const vector<int>& arr) {
    stack<int> stk;
    vector<int> result;

    for (int num : arr) {
        while (!stk.empty() && stk.top() > num) {
            stk.pop();
        }
        stk.push(num);
    }

    while (!stk.empty()) {
        result.insert(result.begin(), stk.top());
        stk.pop();
    }

    return result;
}

// Driver code
int main() {
    vector<int> arr = {1, 4, 5, 3, 14, 17};

    // Function Call
    vector<int> result = increasingStack(arr);

    // Displaying the original array
    cout << "The Original Array: ";
    for (int num : arr) {
        cout << num << " ";
    }
    cout << endl;

    // Displaying Monotonic increasing stack
    cout << "The Monotonic Stack: ";
    for (int num : result) {
        cout << num << " ";
    }
    cout << endl;

    return 0;
}

import java.util.Stack;

public class MonotonicIncreasingStack {

  // Function to build a monotonic increasing stack
  static int[] increasingStack(int[] arr) {
      Stack<Integer> stack = new Stack<>();
      
      for (int num : arr) {
          while (!stack.isEmpty() && stack.peek() > num) {
              stack.pop();
          }
          stack.push(num);
      }

      int n = stack.size();
      int[] result = new int[n];
      int i = n - 1;

      // Empty Stack
      while (!stack.isEmpty()) {
          result[i--] = stack.pop();
      }

      return result;
  }

  // Driver code
  public static void main(String[] args) {
      int[] arr = {1, 4, 5, 3, 14, 17};

      // Function Call
      int[] result = increasingStack(arr);

      // Displaying the original array
      System.out.print("The Original Array: ");
      for (int num : arr) {
          System.out.print(num + " ");
      }
      System.out.println();

      // Displaying Monotonic increasing stack
      System.out.print("The Monotonic Stack: ");
      for (int num : result) {
          System.out.print(num + " ");
      }
      System.out.println();
  }
}

def increasing_stack(arr):
    stack = []
    result = []

    for num in arr:
        while stack and stack[-1] > num:
            stack.pop()
        stack.append(num)

    while stack:
        result.insert(0, stack.pop())

    return result

# Driver code
arr = [1, 4, 5, 3, 14, 17]

# Function Call
result = increasing_stack(arr)

# Displaying the original array
print("The Original Array:", *arr)

# Displaying Monotonic increasing stack
print("The Monotonic Stack:", *result)

using System;
using System.Collections.Generic;

class Program
{
    // Function to build a monotonic increasing stack
    static int[] IncreasingStack(int[] arr)
    {
        Stack<int> stack = new Stack<int>();

        foreach (int num in arr)
        {
            while (stack.Count > 0 && stack.Peek() > num)
            {
                stack.Pop();
            }
            stack.Push(num);
        }

        int n = stack.Count;
        int[] result = new int[n];
        int i = n - 1;

        // Empty Stack
        while (stack.Count > 0)
        {
            result[i--] = stack.Pop();
        }

        return result;
    }

    // Driver code
    static void Main()
    {
        int[] arr = { 1, 4, 5, 3, 14, 17 };

        // Function Call
        int[] result = IncreasingStack(arr);

        // Displaying the original array
        Console.Write("The Original Array: ");
        foreach (int num in arr)
        {
            Console.Write(num + " ");
        }
        Console.WriteLine();

        // Displaying Monotonic increasing stack
        Console.Write("The Monotonic Stack: ");
        foreach (int num in result)
        {
            Console.Write(num + " ");
        }
        Console.WriteLine();
    }
}

Output:

The Original Array: 1 4 5 3 14 17 
The Monotonic Stack: 1 3 14 17 

Time Complexity: O(n)

Space Complexity: O(n)

Advantages of Monotonic Stack.

• It allows quick determination of immediate next or previous elements in a sequence, aiding in optimizing various algorithms.
• It provides a straightforward approach to solving problems involving the next greater/smaller elements or histogram-related calculations.
• It offers improved complexity in scenarios requiring element comparisons, reducing the overall computation time.

Disadvantages of Monotonic Stack.

• It's specialized for problems requiring specific immediate next or previous element computations and might not be suitable for border algorithmic solutions.
• It involves maintaining a stack, which can lead to additional memory overhead in scenarios with large input sizes.

Stack Implementation in Python.

In Python, the stack data structure represents a fundamental and versatile form of collection, adhering to the Last In, First Out (LIFO) principle. It organizes elements in a manner where the last element added is the first one to be removed, resembling a stack of items. Python facilitates stack implementation through its built-in data structures like lists or by utilizing modules from the collections or queue libraries.

Note: Here we will cover stack implementation in Python programming. If you are not familiar with stack data structure then you can check our post "Introduction to Stack Data Structure" in which we have explained the stack in complete detail with code.

Basic Stack Operations.

• push(element): Add/Insert an element onto the stack.
• pop(): Remove the element from the top of the stack.
• peek(): View the top element without removing it.
• empty(): Check if the stack is empty. Return true if the stack is empty.
• size(): Find the number of elements present in the stack.

Implementation of Stack in Python.

There are various methods to implement stack in Python and here we are going to learn three different methods:

• Using List.
• Using collection.deque.
• Using queue.LifoQueue.

Stack Implementation Using List.

The stack implementation in Python using a list mirrors the behavior of a traditional stack data structure by utilizing Python's built-in list functions. Elements are added to the top of the stack, resembling a push operation via the append() method. Similarly, the pop() function removes and returns the top element, replicating the stack's pop operation.

To view the top element without removing it (peek operation), referencing the last element (self.stack[-1]) of the list is employed, providing a glimpse into the topmost element of the stack. The size of the stack is determined by obtaining the length of the underlying list (len(self.stack)), indicating the number of elements present.

However, the implementation has drawbacks. Python lists utilize dynamic arrays, resulting in automatic resizing to accommodate elements. While append() and pop() operations typically offer O(1) time complexity, the occasional resizing might lead to O(n) complexity in specific cases, impacting performance.

Python Code:

class StackUsingList:
    # Initializing an empty list as a stack
    def __init__(self):
        self.stack = []  
    
    # Adding an element to the top of the stack
    def push(self, element):
        self.stack.append(element)  

    # Removing and returning the top element from the stack
    def pop(self):
        if not self.is_empty():
            return self.stack.pop()  
        else:
            return "Stack is empty"
    
    # Returning the top element without removing it
    def peek(self):
        if not self.is_empty():
            return self.stack[-1]  
        else:
            return "Stack is empty"
    
    # Checking if the stack is empty
    def is_empty(self):
        return len(self.stack) == 0  
    
    # Determining the size of the stack
    def size(self):
        return len(self.stack)  

# Example usage:
stack = StackUsingList()
stack.push(10)
stack.push(20)
stack.push(30)

print("Size of stack:", stack.size())  

print("Top element:", stack.peek()) 

print("Popped element:", stack.pop()) 

print("Is stack empty?", stack.is_empty())  

Output:

Size of stack: 3
Top element: 30
Popped element: 30
Is stack empty? False

Stack Implementation Using collection.deque.

The stack implementation using collection.deque in Python provides an efficient alternative to mimic stack behavior while addressing some of the drawbacks of using lists.

Implementation:

• To Initialize an empty dequeue from the collections module to serve as the stack: stack = dequeu().
• To add elements to the stack (push) we use the append() function of deque. This adds elements to the right side of the deque, emulating the stack's push operation.
• To remove or retrieve the top element (pop) from the stack we use pop() function of the deque. This removes and returns the rightmost element, simulating the stack's pop operation.
• To access the top element without removing it (peek) by referencing the rightmost element (stack[-1]) of the deque, providing a view into the top element.
• To verify if the stack is empty we check the length of the deque and if the length is 0 (len(stack) == 0) it means the stack is empty.
• To determine the size of the stack by retrieving the length of the deque (len(stack)), indicating the count of elements in the stack.

Python Code:

from collections import deque

class StackUsingDeque:
    # Initializing an empty deque as a stack
    def __init__(self):
        self.stack = deque()  

    # Adding an element to the top of the stack
    def push(self, element):
        self.stack.append(element)  

    # Removing and returning the top element from the stack
    def pop(self):
        if not self.is_empty():
            return self.stack.pop()  
        else:
            return "Stack is empty"

    # Returning the top element without removing it
    def peek(self):
        if not self.is_empty():
            return self.stack[-1]  
        else:
            return "Stack is empty"
    
    # Checking if the stack is empty
    def is_empty(self):
        return len(self.stack) == 0  
    
    # Determining the size of the stack
    def size(self):
        return len(self.stack)  

# Example usage:
stack = StackUsingDeque()
stack.push(10)
stack.push(20)
stack.push(30)

print("Size of stack:", stack.size())  

print("Top element:", stack.peek())

print("Popped element:", stack.pop())

print("Is stack empty?", stack.is_empty())  

Output:

Size of stack: 3
Top element: 30
Popped element: 30
Is stack empty? False

Stack Implementation using queue.LifoQueue.

The implementation of a stack queue.LifoQueue in Python provides a direct and thread-safe approach to creating a stack data structure adhering to the Last-In, First Out (LIFO) principle. This implementation is part of the queue module, offering synchronization and efficient LIFO-based operations for managing in a stack-like manner.

The functionality of Stack Implementation using the queue.LifoQueue:

• Initialize an empty stack using LifoQueue: stack = LifoQueue(). This creates a stack structure optimized for LIFO operations.
• Add elements onto the stack (push) using the put() method of LifoQueue. Elements are inserted into the stack, following the LIFO order, ensuring the last element added becomes the top of the stack.
• Remove and retrieve elements from the top of the stack(pop) using the get() method of LifoQueue. This retrieves elements in the reverse order of their insertion, effectively mimicking the behavior of a stack.
• Accessing the top element of the stack without removing it (peek) by using not_empty() attribute allows viewing the top element without altering the stack contents.
• Obtain the size of the stack using the qsize() method of LifoQueue, which retrieves the count of elements present in the stack.

Python Code:

from queue import LifoQueue

# Initializing a LifoQueue as a stack
class StackUsingLifoQueue:
    def __init__(self):
        self.stack = LifoQueue()

    # Adding an element to the top of the stack
    def push(self, element):
        self.stack.put(element)

    # Removing and returning the top element from the stack
    def pop(self):
        if not self.is_empty():
            return self.stack.get()  
        else:
            return "Stack is empty"

    def peek(self):
        if not self.is_empty():
            top_element = self.stack.get()
            # Restoring the element after peeking
            self.stack.put(top_element)
            # Returning the top element without removing it  
            return top_element  
        else:
            return "Stack is empty"

    # Checking if the stack is empty
    def is_empty(self):
        return self.stack.empty()  
     
    # Determining the size of the stack
    def size(self):
        return self.stack.qsize()

# Example usage:
stack = StackUsingLifoQueue()
stack.push(10)
stack.push(20)
stack.push(30)

stack.push(40)

print("Size of stack:", stack.size()) 

print("Top element:", stack.peek())  

print("Popped element:", stack.pop())  

print("Is stack empty?", stack.is_empty())  

Output:

Size of stack: 4
Top element: 40
Popped element: 40
Is stack empty? False

I hope now you understand three different ways to implement stack data structure in Python. Stack is a very useful data structure and have many applications in numerous domains, from handling function calls to algorithmic problem-solving, making it an essential component in Python programming.