Quick Sort Algorithm in C++.

In our previous post, we discussed Merge Sort Algorithm and we know that Merge Sort Algorithm has O(nlogn) time complexity in the worse case and it is an in-place algorithm with O(n) space complexity. 

Here in this post, we are going to discuss the Quick Sort Algorithm which is a recursive algorithm whose average case time complexity is O(nlogn) and worse case time complexity is O(n^2) but unlike merge sort, it is an in-place algorithm with O(1) space complexity. 

Note: Quick Sort has O(n^2) time complexity in the worse case but it is much more efficient in practical scenarios that we can ignore the worse case running time by using a randomized version of Quick Sort. Sort function which is available for us by most of the programming language libraries is implemented using Quick Sort.(alert-success)

Working of Quick Sort Algorithm.

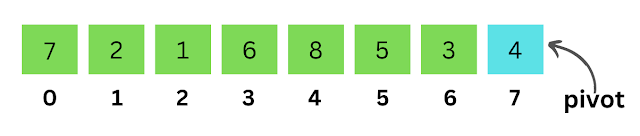
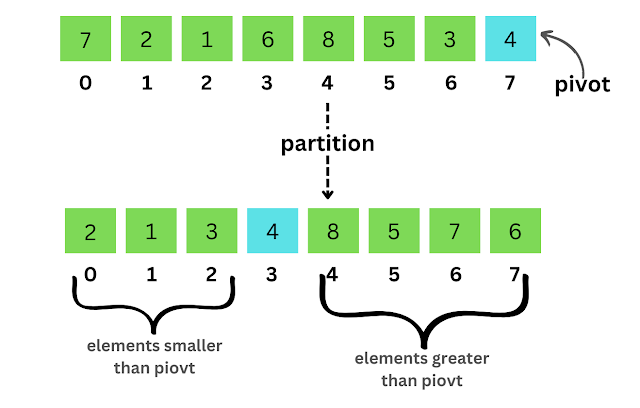
In the Quick Sort algorithm, we first select one element from the given array and there are no strict rules for picking this element we can pick any element. Now let's say we picked the last element and consider this as a pivot of our algorithm. 

Our next step is that we need to re-arrange the given array such that all the elements smaller than the pivot are moved towards the left side of the pivot and all the elements greater than the pivot are moved towards the right of the pivot. This process is known as the partitioning of the given array. All the rearrangements are happening in the original array only.

Once the partitioning is done for the given array we can break our problem into two sub-problem where we need to sort the segment of the array present on the left side of the pivot and we need to sort the segment of the array present on the right side of the pivot. We repeat this process recursively until we are left with no or only one element. 

Algorithm of Quick Sort.

QuickSort(Array[], start, end)

{

    if(start >= end) return;

    pindex = partition(Array[], start, end);

    QuickSort(Array[], start, pindex-1);//Before pivot

    QuickSort(Array[], pindex+1, high);//After pivot

}(alert-passed)

Working of Partition Algorithm.

Let's say the last element of the array is our pivot element and by partitioning, we will move all smaller elements to the left side of the pivot and all greater elements to the right side of the pivot. By using this algorithm each time we are placing the pivot element to its correct location in our array.

Algorithm of Partition.

Partition(Array[], start, end)

{

   pivot = Array[end];

   pindex = start;

   for(i  = start to end -1)

   { 

     if(Array[i] <= pivot)

     {

        swap(Array[i], Array[pindex]);

        pindex = pindex+1;

     }

   }

   swap(Array[pindex], Array[end]);

   return pindex;

}(alert-passed)

C++ Code Implementation of Quick Sort Algorithm.

//C++ Code for Quick Sort Algorithm
#include<iostream>
using namespace std;

/*
Partition function taken last element as a pivot
and place the pivot at its correct location in the
given array by arrranging all smaller element to 
left side of pivot and all greater element to right
side of pivot.
*/
int partition(int arr[], int start, int end){
    //pivot element
    int pivot = arr[end];
    int pindex = start;

    for(int i = start; i < end; i++){
        //current element is smaller than or equal to pivot
        if(arr[i] <= pivot){
            swap(arr[i], arr[pindex]);
            pindex = pindex+1;
        }
    }
    swap(arr[pindex], arr[end]);
    return pindex;
}
//Recursive Quick Sort function
void quickSort(int arr[], int start, int end){
    //base case
    if(start >= end) return;
    /*pindex is partitioning index or it is 
     the correct position of pivot element*/
    int pindex = partition(arr, start, end);
    quickSort(arr, start, pindex-1); //sorting before pivot
    quickSort(arr, pindex+1, end); //sorting after pivot
}

int main(){
    int arr[] = {7, 2, 1, 6, 8, 5, 3, 4};
    //Size of given array
    int n = sizeof(arr)/sizeof(arr[0]);

    cout<<"Array Before Sorting: ";
    for(int i = 0; i < n; i++){
        cout<<arr[i]<<" ";
    }

    quickSort(arr, 0, n-1);

    cout<<"\nArray After Sorting: ";
    for(int i = 0; i < n; i++){
        cout<<arr[i]<<" ";
    }
}

Output:

Array Before Sorting: 7 2 1 6 8 5 3 4
Array After Sorting: 1 2 3 4 5 6 7 8

• Time Complexity: The average case time complexity of the QuickSort algorithm is O(nlogn) and the worst case time complexity is O(n^2). 
• Space Complexity: The space complexity of the Quick Sort algorithm is O(1) because of all the operations of and the arrangement was happing in the same given array. 

Quick sort is not a stable sorting algorithm because in a stable sorting algorithm the relative order of records with equal keys is preserved.

See more:

(getButton) #text=(Insertion Sort Algorithm) #icon=(link) #color=(#2339bd)

(getButton) #text=(Bubble Sort Algorithm) #icon=(link) #color=(#2339bd)

How To Add Signature in Gmail.

Gmail is now the most popular emails providers for many small and large businesses and for personal usage. It provides us many useful features that most Gmail users hardly use such as Gmail's Signature feature. Yes, you heard it right our favorite Gmail provides us an option to add our signature to every email we send. 

In this blog post, we are going to learn how we can automatically add our signature to every email we send or reply from Gmail.

Why do we need a Gmail Signature?

Adding a signature to any email adds recognization and authentication because it contains information about you or your company. The signature can contain details like your name your profession or the company name in which you are working or it can contain details of your social media links.

Steps to Add a Signature in Gmail.

Open your Gmail Account and click on the Settings icon in the top right corner and then click on "See all settings". 

Under General settings scroll the page a little down and search for the "Signature" option and click on "Create new".

You will get one popup inbox to give a name to your signature. Fill in any name of your own choice and click on "Create".

Add your Gmail signature inside the given box and you can also use other given features to customize your signature by adding images and social media links.

You can check your signature default option just below create a new button and from the drop-down, you can select the name of your signature. There you will notice one checkbox "Insert signature before quoted text in replies and remove the "--" line that precedes it" check this box to add your signature to all your replies.

Now, whenever you will try to send any email your default signature will get added and if you want to remove the signature for any particular email then you can choose the quick option "Manage signature" and choose the "No signature" option from the drop-down.

I hope you have learned the complete process of adding your signature to your Gmail but if you still face any difficulties please them in the comment section below and please do share this post if you really found this useful.

(getButton) #text=(How To Send a Confidential Email in Gmail) #icon=(link) #color=(#2339bd)

Program to Find the Sum of all Array Elements in C++.

Given an Array of integers of size n. Find the Sum of all the elements present in the given Array.

Example 1: 
Input: arr[] = {2, 5, 9, 7, 10}
Output: 33
Explanation: 2 + 5 + 9 + 7 + 10 = 33

Example 2: 
Input: arr[] = {5, -2, 10, 7, 2}
Output: 22
Explanation: 5 + (- 2) + 10 + 7 + 2 = 22

Method 1: Iterative method using for loop.

Steps to find the Sum of Array elements:

• Declare one sum variable to store the sum of the array and initialize it with 0.  
• Run a for loop through all the array elements and keep on adding them one by one to sum the variable.(sum = sum + arr[i])
• Print the value of the sum. 

C++ Program to find the sum of all Array Elements.

//C++ Program to find sum of array elements
#include<iostream>
using namespace std;

//Function to return sum of array
int sum(int arr[], int n){
    int sum = 0;

    for(int i = 0; i < n; i++){
        sum = sum + arr[i];
    }

    return sum;
}

int main(){
    int arr[] = {2, 5, 9, 7, 10};
    //size of given array
    int n = sizeof(arr)/sizeof(arr[0]);

    cout<<"Sum of Array Elements: "<<sum(arr, n);
}

Output:

Sum of Array Elements: 33

• Time Complexity: O(n)
• Space Complexity: O(1)

Method 2: Using Recursion.

The base case of our recursive function is when the size of the array will become 0 and until we hit the base case we keep on calling our sum function each this by decreasing the size of the array by one.

//C++ Program to find sum of array elements
#include<iostream>
using namespace std;

//Recursive Function to return sum of array
int sum(int arr[], int n){
    //base case
    if(n == 0){
        return 0;
    }
    else{
        //Calling the function recursively
        return arr[0] + sum(arr+1, n-1);
    }
}

int main(){
    int arr[] = {2, 5, 9, 7, 10};
    //size of given array
    int n = sizeof(arr)/sizeof(arr[0]);

    cout<<"Sum of Array Elements: "<<sum(arr, n);
}

Output:

Sum of Array Elements: 33

• Time Complexity: O(n)
• Space Complexity: O(1)

Merge Sort Algorithm in C++ | Visualization

The Merge Sort Algorithm is a sorting algorithm that uses the Divide and conquer technique to sort the array elements in ascending or descending order. In this algorithm, we break our problem into sub-problems then we try to merge the solution of the sub-problem to get the solution of our main problem. 

Working of Merge Sort Algorithm.

The merge Sort approach is entirely different than other sorting algorithms like Selection sort, Bubble sort, and Insertion sort where the time complexity of these algorithms is O(n^2) in the average case our Merge sort algorithm's time complexity is O(nlogn).

Here we divide the given unsorted array into two equal halves (if an array has an odd number of elements then one half will have more elements than the other half) then we apply some algorithm to sort these two equal halves and we merge these two halves in sorted order. 

Now if you observe carefully, we have two tasks one is to sort the two halves and the next is to merge the two sorted sub-array in a bigger array but in sorted order. We are going to use Recursion to perform this dividing of the array into two equal parts because we will keep on diving the array until no further division is possible and while returning back we are going to perform the merge operation.

Lets us first understand how the merge operation is going to take place when we already have two sorted sub-array. 

Let's say we named two sorted sub-array as the left sub-array (left[]), and the other as the right sub-array (right[]). Since all the elements of the given array, Arr[] are present either in the left sub-array or right sub-array so we will start picking the smallest element either from the left or right sub-array and start overwriting in the given Array Arr[]

.  

Algorithm to Merge Two-Sorted Arrays:

Step 1: Get the size of the left subarray and right subarray.

Step 2: Declare three variables i, j, and k, and initialize them with 0.

Step 3: Run a while loop with the below condition to merge two sorted arrays:

while(i < left_subarray_size && j < right_subarray_size){
        if(left[i] <= right[j]){
            arr[k] = left[i];
            k++;
            i++;
        }
        else{
            arr[k] = right[j];
            k++;
            j++;
        }
    }

Step 4: The above while loop condition will fail when we meet a condition where no elements are present to compare either in the left subarray or in the right subarray. In this case, we have picked all the elements of the other array and filled the rest of the position. We can run two different while loops for both left and right subarrays.

//copy the remaining elements from left subarray if any.
    while(i < left_subarray_size){
        arr[k] = left[i];
        i++;
        k++;
    }
    //copy the remaining elements from right subarray if any.
    while(j < right_subarray_size){
        arr[k] = right[j];
        j++;
        k++;
    }

Now after understanding the algorithm of merging two sorted arrays and combining them into a single larger sorted array. It is the right to understand the working of the Merge sort algorithm and then only you will understand why it was necessary to understand the above merging algorithm before. 

Basically, Merge Sort is a recursive algorithm in which we continually divide the given unsorted array into equal two parts until it cannot further divide. We will get this case when there is only one element left or the array is empty and it is our base case of recursion. When we hit the base case and start returning we will start merging both sorted halves into a larger array until the entire array is merged. This is where we will use the above algorithm of merging two sorted arrays. 

Steps to perform Merge Sort Algorithm.

Step 1: Call a recursive mergesort(arr[], l, r) with given array and one left variable and one right variable. 

Step 2: If left >= right then we hit the base case and you need to return.

Step 3: If left < right then we have need to perform the below task.

Step 4: Find the middle to divide the array into equal halves. 

• mid = left + (right - left)/2

Step 5: Call mergersort again on first half.

• mergesort(arr[], left, mid);

Step 6: Call mergersort again on second half.

• mergesort(arr[], mid+1, right);

Step 7: Call merge function to merge two sorted half together (as shown above).

• merge(arr[], left, mid, right);(alert-success)

C++ Code Implementation for Merge Sort Algorithm.

#include<iostream>
using namespace std;

//function to merge two sorted array
void merge(int arr[], int left, int mid, int right){
    
    int left_subarray_size = mid - left + 1;
    int right_subarray_size = right - mid;

    int leftArr[left_subarray_size];
    int rightArr[right_subarray_size];

    //copying data of left and right subarray from main array
    for(int i = 0; i < left_subarray_size; i++){
        leftArr[i] = arr[left+i];
    }
    for(int j = 0; j < right_subarray_size; j++){
        rightArr[j] = arr[mid+j+1];
    }

    int i = 0, j = 0, k = left;
    //Merging left and right sorted array into main array
    while(i < left_subarray_size && j < right_subarray_size){
        if(leftArr[i] <= rightArr[j]){
            arr[k] = leftArr[i];
            k++;
            i++;
        }
        else{
            arr[k] = rightArr[j];
            k++;
            j++;
        }
    }

    //copy the remaining elements from left subarray.
    while(i < left_subarray_size){
        arr[k] = leftArr[i];
        i++;
        k++;
    }
    //copy the remaining elements from right subarray.
    while(j < right_subarray_size){
        arr[k] = rightArr[j];
        j++;
        k++;
    }
}
//MergeSort Recursive Function
void mergeSort(int arr[], int left, int right){
   
    if(left >= right)
       return;
    
    int mid = left + (right - left)/2;   

    //Calling mergeSort recursively on both halves
    mergeSort(arr, left, mid);
    mergeSort(arr, mid+1, right);
    merge(arr, left, mid, right);
}

int main(){
    int arr[] = {2, 4, 1, 6, 8, 5, 3, 7};
    int n = sizeof(arr)/sizeof(arr[0]);

    cout<<"Array before Sorting: ";
    for(int i = 0; i < n; i++){
        cout<<arr[i]<<" ";
    }

    //Calling Merge Sort Function
    mergeSort(arr, 0, n-1);
    
    cout<<"\nArray after Sorting: ";
    for(int i = 0; i < n; i++){
        cout<<arr[i]<<" ";
    }
}

Output

Array before Sorting: 2 4 1 6 8 5 3 7
Array after Sorting: 1 2 3 4 5 6 7 8

• Time complexity: O(NlogN)
• Space Complexity: O(N)

In merge sort, extra space is required because we need to copy the given array into auxiliary space for sorting and it is a stable sorting algorithm. But merge sort is not a good choice for the smaller data units.

Insertion Sort Algorithm in C++.

The insertion Sort Algorithm is one of the simple (but not the best) sorting algorithms that is used to sort the array elements in ascending or descending order. In this article, we are going to understand the working and code implementation of this algorithm.

Insertion sort working is very similar to the way we sort playing cards in our hands. We assume that our first card is sorted and we will try to place our remaining unsorted cards in their correct position. In Insertion sort, an array is divided into sorted and unsorted parts and we have to take the elements from the unsorted part and place them in the sorted part of the array. This sorting algorithm is adaptive in nature and best for the data set which is partially sorted.

Working of Insertion Sort Algorithm.

Steps for Insertion Sort Algorithm.

Step 1: Run a loop to iterate all the elements of the array from 1 to n.

Step 2: Divide the given array into sorted and unsorted parts and assume that the first element is present in the sorted part of the array. 

Step 3: Pick the first element from the unsorted part of the array and compare it with elements present in the sorted part. 

Step 4: If you find all the elements present in the sorted part are smaller than the current element then include the current element into the sorted part and move to the next element, else find the correct position of the current element in the sorted part of the array and shift all the greater elements one unit right side to make space to insert the current element.

Step 5: Repeat the above steps until the entire array gets sorted. 

C++ Code Implementation for Insertion Sort Algorithm.

#include<iostream>
using namespace std;

//function for insertion sort
void insertionSort(int arr[], int n){
    int key, j;

    for(int i = 1; i < n; i++){
        key = arr[i];
        j = i-1;

        /*
        Moving the elements one position right
        that are greater than key to make space
        for key
        */
        while (j >= 0 && arr[j] > key)
        {
            arr[j+1] = arr[j];
            j = j-1;
        }
        arr[j+1] = key;
    }
}
int main(){
    int arr[] = {7, 2, 4, 1, 5, 3};
    //size of given array
    int n = sizeof(arr)/sizeof(arr[0]);

    insertionSort(arr, n);

    //Printing the sorted Array
    cout<<"Sorted Array: ";
    for(int i = 0; i < n; i++){
        cout<<arr[i]<<" ";
    }
}

Output:

Sorted Array: 1 2 3 4 5 7

• Time Complexity: O(n^2)
• Space Complexity: O(1)

Insertion sort is an in-place and stable sorting algorithm that works better than selection sort and bubble sort when the number of elements is small and partially sorted.  

See more:

(getButton) #text=(Merge Sort Algorithm) #icon=(link) #color=(#2339bd)

(getButton) #text=(Quick Sort Algorithm) #icon=(link) #color=(#2339bd)

How to Lock Google Chrome Incognito Mode with Fingerprint.

Google Chrome is now providing an interesting feature of putting a Fingerprint lock on Incognito Mode whenever you exit the tabs. This feature is going to make Incognito mode safer and private for browsing by providing this extra layer of security. 

This is now only available on Andriod Google Chrome and it is very useful when you are in a situation of sharing your mobile with someone else. All Incognito tabs will automatically get locked as soon as you exit the tabs and when you try to reopen those tabs you will get one black screen with the "Unlock Incognito" button. You need to tap on that button and it will ask you for your fingerprint.

Steps to put Fingerprint Lock on Incognito Mode.

1. Open your Google Chrome Browser on your Android Device and type "chorme://flags".

2. You can see one search box on top, type "incognito-reauthentication-for-android". Once you get this option you need to select the drop-down menu and choose Enabled. Relaunch the Chrome Browser. 

3. Click on the three dots in the upper right corner of Google Chrome and select "Settings".

4. Inside the Settings option, you need to choose the "Privacy and Security" option.

5. You need to enable the toggle option "Lock Incognito tabs when you leave Chrome" and Done.

6. To unlock your locked tabs you need to click on "Unlock Incognito" on the screen and give your fingerprint.

Now your Incognito mode is ready to use privately with biometric authentication security. This feature is not by default present in Chrome settings so do share this post with other people so they can also make use of this cool trick.

Bubble Sort Algorithm in C++.

The Bubble Sort is one of the popular and easy Sorting algorithms used to arrange the array of elements in ascending or descending order. In Bubble Sort Algorithm, we continuously keep on swapping two adjacent elements if they are present in the incorrect order. The worst-case time complexity of this algorithm is very high so it is not considered a suitable algorithm when there is a huge amount of data. 

Working of Bubble Sort Algorithm.

Steps for Bubble Sort Algorithm (Ascending Order):

• Run two nested loops and traverse the given array where the outer loop will run n-1 times and the inner loop will run n-i-1 times.
• In each iteration, we will pick two adjacent elements of the array and if arr[j] > arr[j+1] then we will swap their position else we will move to the next adjacent element. After completing each iteration the greatest element will move to the right end of the array.
• In the end, you will see that no swapping is required and all elements are arranged in sorted order.

Below is the C++ Code Implementation of the Bubble Sort Algorithm.

#include<iostream>
using namespace std;

//Implementation of Bubble Sort
void bubbleSort(int arr[], int n){

    for(int i = 0; i < n-1; i++){
        for(int j = 0; j < n-i-1; j++){
            //Comparing two adjacent element
            if(arr[j] > arr[j+1]){
                swap(arr[j], arr[j+1]);
            }
        }
    }
}

int main(){
    int arr[] = {10, 23, 5, 8, 21, 15};
    //size of given array
    int n = sizeof(arr)/sizeof(arr[0]);

    bubbleSort(arr, n);

    cout<<"Sorted Array:";
    for(int i = 0; i < n; i++){
        cout<<arr[i]<<" ";
    }
}

Output:

Sorted Array:5 8 10 15 21 23

• Time Complexity: O(n^2)
• Space Complexity: O(1)

See more:

(getButton) #text=(Selection Sort Algorithm) #icon=(link) #color=(#2339bd)

(getButton) #text=(Insertion Sort Algorithm) #icon=(link) #color=(#2339bd)

(getButton) #text=(Merge Sort Algorithm) #icon=(link) #color=(#2339bd)

(getButton) #text=(Quick Sort Algorithm) #icon=(link) #color=(#2339bd)