Breadth First Search (BFS) is a graph traversal algorithm that visits all the vertices of a graph in breadth-first order, meaning that it visits all the vertices at the same level before moving on to the next level. The algorithm uses a queue data structure to keep track of the vertices that need to be visited.
How BFS for Graph is different from BFS for Tree Data structure?
The main difference between the graph and the tree BFS traversal is that a tree cannot contain cycles but a graph can contain cycles. To avoid visiting the same vertex again and again we use a boolean visited array to mark the visited vertices.
If we don't mark the visited vertices, the algorithm may revisit vertices that have already been explored and get stuck in an infinite loop. This is especially true in the case of cycles, where a BFS traversal without marking visited vertices could result in an infinite loop.
Algorithm of Breadth First Search:
- Step 1: Create a queue data structure and add the starting vertex to the queue.
- Step 2: While the queue is not empty:
- Step 3: Dequeue the vertex at the front of the queue and mark it as visited.
- Step 4: Visit all the unvisited neighbors of the dequeued vertex and add them to the queue.
- Step 5: If all the vertices have been visited, the algorithm is complete.
Example with Illustration.
 |
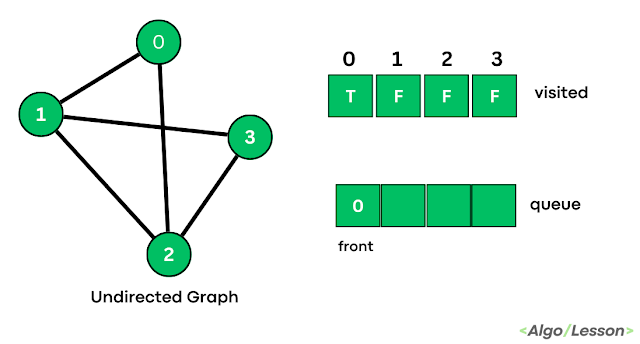| Step 1 |
 |
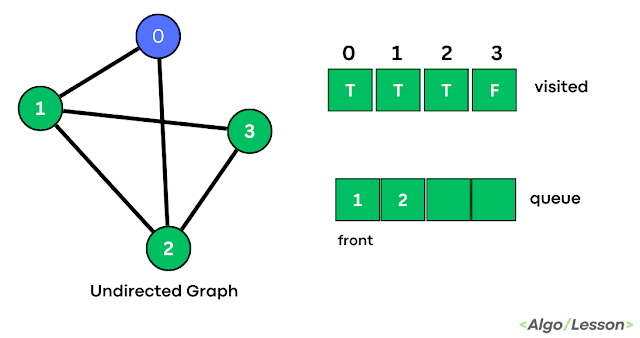| Step 2 |
Pop the front element 0 from the queue and print it. Push the adjacent vertices 1 and 2 inside the queue and then mark them as visited.
 |
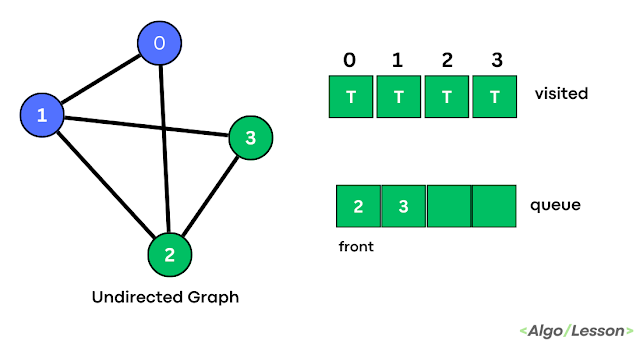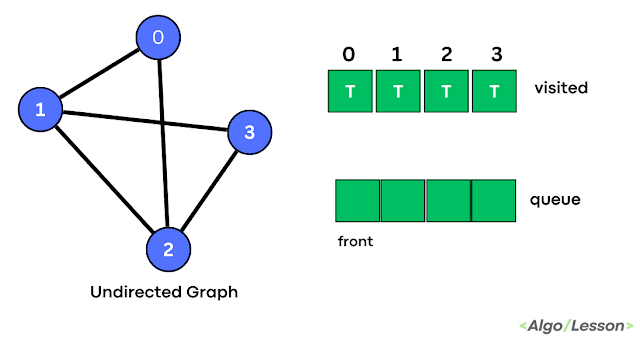
| Step 3 |
Pop the front element 1 from the queue and print it. Push the adjacent vertices 2 and 3 inside the queue but 2 is already visited so push only 3 and then mark them as visited.
 |
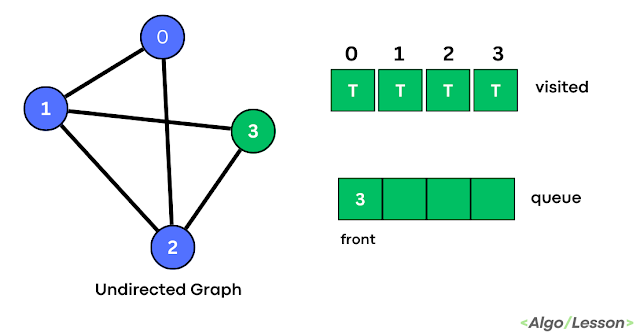| Step 4 |
 |
| Step 5 |
C++ Code for BFS Traversal Using Queue.
Here is an example of BFS implementation in C++ for an undirected graph represented as an adjacency list:
//C++ Code for BFS Traversal of Undirected Graph #include <iostream> #include <vector> #include <queue> using namespace std; //breadth first search of traversal void bfs(int V, vector<int> adj_list[], int start) { vector<bool> visited(V, false); queue<int> q; visited[start] = true; q.push(start); while (!q.empty()) { int current_vertex = q.front(); q.pop(); cout << current_vertex << " "; for (auto neighbor : adj_list[current_vertex]) { if (!visited[neighbor]) { visited[neighbor] = true; q.push(neighbor); } } } } int main() { int V = 4; vector<int> adj_list[V]; adj_list[0] = {1, 2}; adj_list[1] = {0, 2, 3}; adj_list[2] = {0, 1, 3}; adj_list[3] = {1, 2}; bfs(V, adj_list, 0); return 0; }
0 1 2 3- Time Complexity: O(V + E) where V is the number of vertices and E is the number of edges.
- Space Complexity: O(V) where one visited array of size V is used to mark visited vertices and one queue to store adjacent vertices while traversing.
BFS Traversal for Disconnected Graph.
The above code for BFS Traversal will not work if the given graph is disconnected. To understand this concept we first have to understand what is disconnected graph.
Disconnected Graph.
A disconnected graph is a graph in which there is no path between at least two vertices. In other words, a disconnected graph can be split into two or more connected components, where each component contains a group of vertices that are connected to each other but not connected to the vertices in other components.
Example:
 |
| Disconnected Graph |
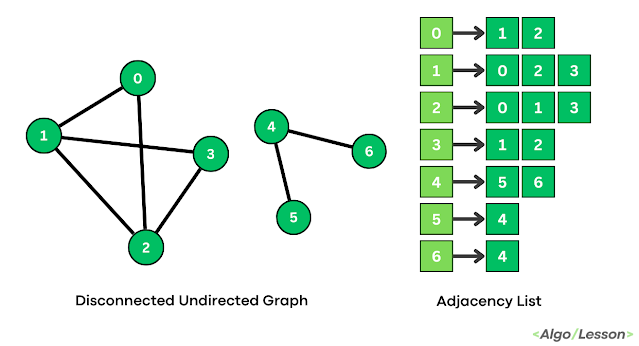We can traverse the disconnected graph by modifying the above BFS code. Below is the C++ code implementation for the BFS traversal of the disconnected graph.
//C++ Code for BFS Traversal of disconnected graph #include <iostream> #include <vector> #include <queue> using namespace std; //breadth first search of traversal void bfs(int V, vector<int> adj_list[], int start, vector<bool> &visited) { queue<int> q; visited[start] = true; q.push(start); while (!q.empty()) { int current_vertex = q.front(); q.pop(); cout << current_vertex << " "; for (auto neighbor : adj_list[current_vertex]) { if (!visited[neighbor]) { visited[neighbor] = true; q.push(neighbor); } } } } int main() { int V = 7; vector<int> adj_list[V]; adj_list[0] = {1, 2}; adj_list[1] = {0, 2, 3}; adj_list[2] = {0, 1, 3}; adj_list[3] = {1, 2}; adj_list[4] = {5, 6}; adj_list[5] = {4}; adj_list[6] = {4}; vector<bool> visited(V, false); //for disconnected graph for(int i = 0; i < V; i++){ if(!visited[i]){ bfs(V, adj_list, i, visited); } } return 0; }
0 1 2 3 4 5 6- Time Complexity: O(V + E) where V is the number of vertices and E is the number of edges.
- Space Complexity: O(V) because we are using a visited array of size V and a queue data structure to store adjacent vertices and it is taken at max V size.
.png "Bipartite Graph")
Trends is an amazing magazine Blogger theme that is easy to customize and change to fit your needs.