Windows shortcuts are an incredibly powerful and efficient way to navigate and control your PC. They allow you to quickly perform tasks and access features without having to waste time clicking through menus or using a mouse. In this article, we will cover 10 essential Windows shortcuts that every user should know.
Windows Key + D
The Windows Key + D shortcut will quickly minimize all open windows and take you straight to your desktop. This is a handy shortcut when you need to access files or folders on your desktop or when you want to quickly switch between applications.
Windows Key + E
The Windows Key + E shortcut will launch Windows Explorer, giving you quick access to all of your files and folders. This is a great way to quickly browse through your files and find what you need without having to open up individual folders.
Windows Key + L
The Windows Key + L shortcut is a quick way to lock your computer when you need to step away from your desk. This is a useful shortcut if you work in an office or public space and want to keep your computer secure.
Windows Key + R
The Windows Key + R shortcut will open the Run dialog box, allowing you to quickly launch programs, files, and folders by typing in their names. This is a great way to quickly access programs or files that you use frequently.
Ctrl + C / Ctrl + X / Ctrl + V
These are the three most common keyboard shortcuts used for copying, cutting, and pasting. Simply select the text or files you want to copy or cut, use Ctrl + C or Ctrl + X, then navigate to where you want to paste the text or files and use Ctrl + V.
Windows Key + Tab
The Windows Key + Tab shortcut is a great way to quickly switch between open applications. It works similarly to Alt + Tab, but with a more visual interface that allows you to see all of your open windows at once.
Ctrl + Z / Ctrl + Y
These shortcuts are used for undoing and redoing actions. If you make a mistake, use Ctrl + Z to undo your last action. If you change your mind and want to redo your action, use Ctrl + Y.
Windows Key + I
The Windows Key + I shortcut will open the Settings app, which is the central hub for managing your Windows settings. From here, you can manage everything from your display settings to your security and privacy settings.
Alt + F4
The Alt + F4 shortcut is a quick way to close an open application. It is a great way to quickly shut down a program that has frozen or is not responding.
Ctrl + Shift + Esc
The Ctrl + Shift + Esc shortcut will open the Task Manager, which is a powerful tool for managing and monitoring your system processes. You can use the Task Manager to see which applications are using the most resources and to close any programs that are causing problems.
Conclusion.
These 10 essential Windows shortcuts will help you navigate and control your PC more efficiently. By using these shortcuts, you can save time and streamline your workflow, making you a more productive and efficient computer user.








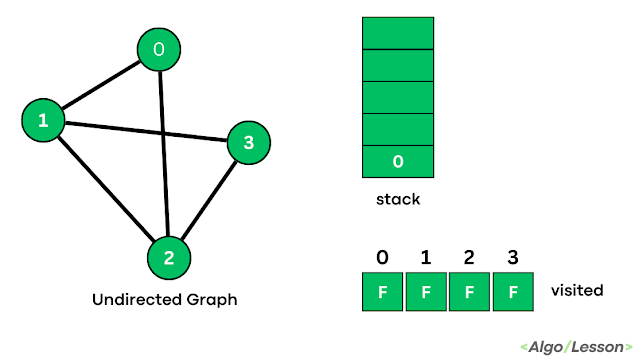
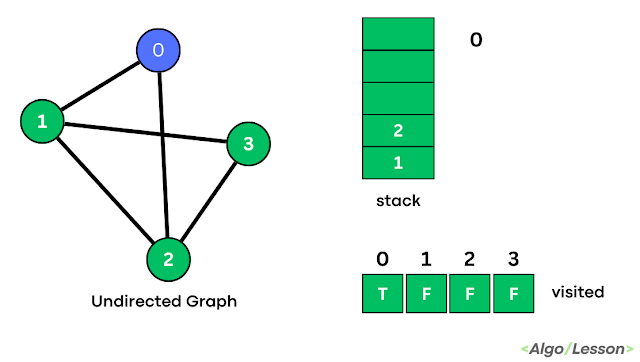

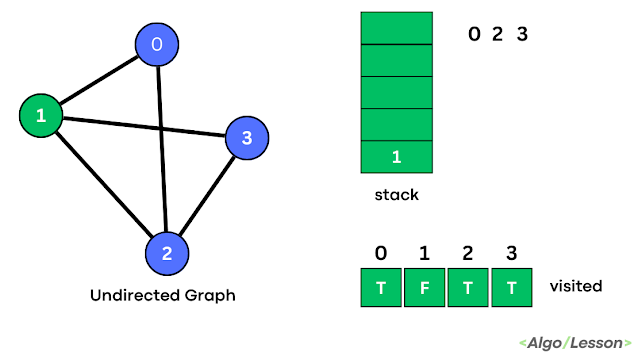
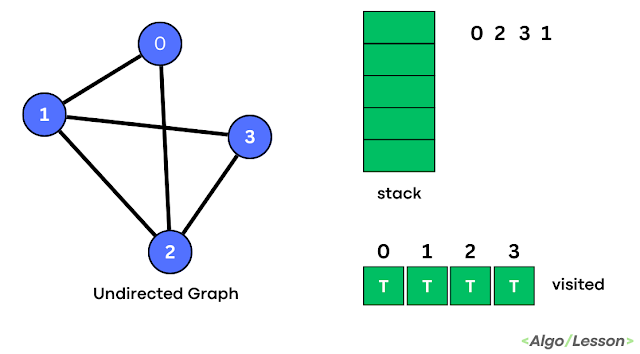
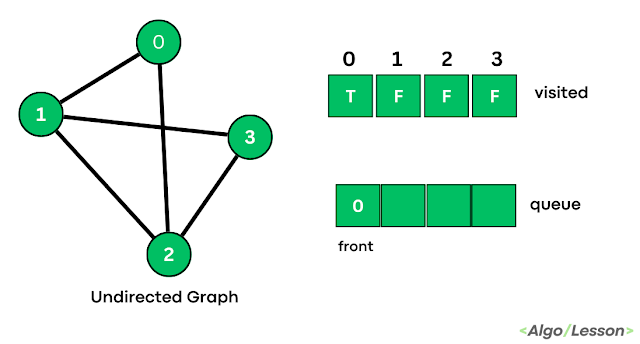
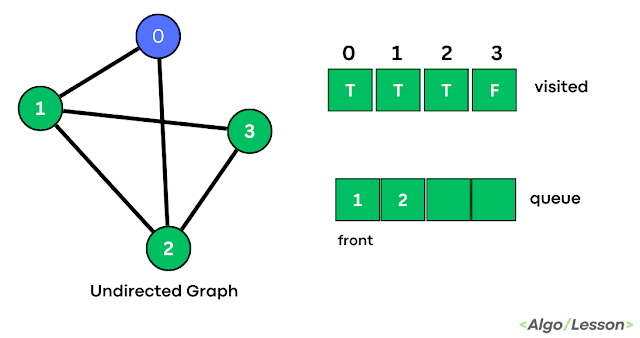
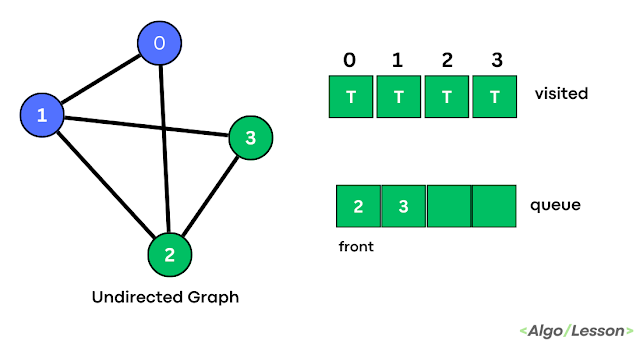
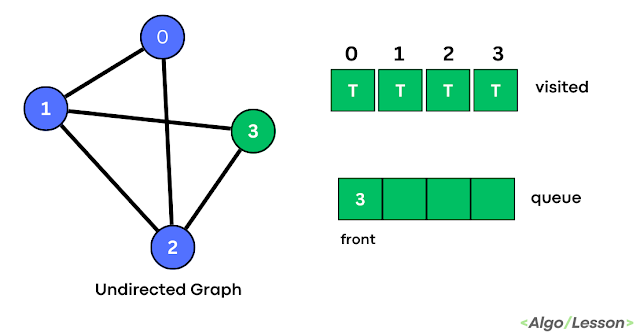







 Trends is an amazing magazine Blogger theme that is easy to customize and change to fit your needs.
Trends is an amazing magazine Blogger theme that is easy to customize and change to fit your needs.