Stack Implementation Using Queues.

Stack is a linear data structure that can be implemented using many other data structures like array and linked list. In this article, we will use a Queue data structure to implement the stack operations that follow the LIFO (Last In, First Out) principle. 

Implementation of Stack Using Queue.

If you are a little bit familiar with stack and queue data structure you might know that in stack insertion and deletion of elements happen only from one top end and in queue insertion of an element happens from the rear end and deletion happens from the front. 

There are two common approaches to implementing a stack using queues:

• Using Two Queues.
• Using Single Queue.

Let's explore both the approaches,

Stack Implementation Using Two Queues.

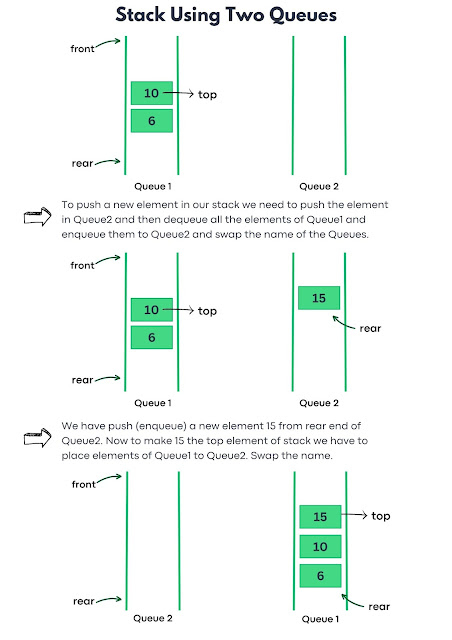
Implementing a stack using two queues involves using one queue (Queue1) for storage and the other (Queue2) for assisting in simulating the Last In, First Out (LIFO) behavior of a stack. 

Push Operation: When pushing an element onto the stack, the new element is enqueued into Queue1, the primary storage queue. To maintain the LIFO order, elements from Queue2, if any, are dequeued and enqueued into Queue1. This step effectively reorganizes the elements to ensure the new addition becomes the topmost element in the simulated stack structure.

Pop Operation: Popping an element from the stack involves dequeuing elements from Queue1 until only one element remains. The objective is to remove the top element, mimicking the behavior of a typical stack operation. By continually dequeuing elements and enqueuing them back into Queue1, except for the last remaining element, the desired element to be removed is identified and dequeued.

Illustration:

Code for Stack Implementation Using Queues.

Below is the code implementation of the above approach:

C++ Java Python C#

// C++ program to implement stack using two Queue
#include <iostream>
#include <queue>
using namespace std;

class Stack {
private:
    queue<int> q1, q2;

public:
    // Push operation
    void push(int value) {
        q1.push(value);
    }

    // Pop operation
    void pop() {
        if (isEmpty()) {
            cout << "Stack is empty. Cannot pop." << endl;
            return;
        }

        // Move elements from q1 to q2, except the last element
        while (q1.size() > 1) {
            q2.push(q1.front());
            q1.pop();
        }

        // Pop the last element from q1
        q1.pop();

        // Swap the names of q1 and q2
        swap(q1, q2);
    }

    // Check if the stack is empty
    bool isEmpty() {
        return q1.empty();
    }

    // Display the top element of the stack
    void peek() {
        if (isEmpty()) {
            cout << "Stack is empty." << endl;
            return;
        }

        // Move elements from q1 to q2, except the last element
        while (q1.size() > 1) {
            q2.push(q1.front());
            q1.pop();
        }

        // Peek at the last element in q1
        cout << "Top element: " << q1.front() << endl;

        // Move the last element back to q1
        q2.push(q1.front());
        q1.pop();

        // Swap the names of q1 and q2
        swap(q1, q2);
    }
};

int main() {
    // Example usage of the stack
    Stack stack;

    // Push elements onto the stack
    stack.push(1);
    stack.push(2);
    stack.push(3);

    // Display the top element
    stack.peek();

    // Pop an element
    stack.pop();

    // Display the top element after pop
    stack.peek();

    return 0;
}

// Java code implementation for stack using Two Queue
import java.util.LinkedList;
import java.util.Queue;

public class Main {
    static class Stack {
        private Queue<Integer> q1 = new LinkedList<>();
        private Queue<Integer> q2 = new LinkedList<>();

        // Push operation
        void push(int value) {
            q1.add(value);
        }

        // Pop operation
        void pop() {
            if (isEmpty()) {
                System.out.println("Stack is empty. Cannot pop.");
                return;
            }

            // Move elements from q1 to q2, except the last element
            while (q1.size() > 1) {
                q2.add(q1.poll());
            }

            // Pop the last element from q1
            q1.poll();

            // Swap the names of q1 and q2
            Queue<Integer> temp = q1;
            q1 = q2;
            q2 = temp;
        }

        // Check if the stack is empty
        boolean isEmpty() {
            return q1.isEmpty();
        }

        // Display the top element of the stack
        void peek() {
            if (isEmpty()) {
                System.out.println("Stack is empty.");
                return;
            }

            // Move elements from q1 to q2, except the last element
            while (q1.size() > 1) {
                q2.add(q1.poll());
            }

            // Peek at the last element in q1
            System.out.println("Top element: " + q1.peek());

            // Move the last element back to q1
            q2.add(q1.poll());

            // Swap the names of q1 and q2
            Queue<Integer> temp = q1;
            q1 = q2;
            q2 = temp;
        }
    }

    public static void main(String[] args) {
        // Example usage of the stack
        Stack stack = new Stack();

        // Push elements onto the stack
        stack.push(1);
        stack.push(2);
        stack.push(3);

        // Display the top element
        stack.peek();

        // Pop an element
        stack.pop();

        // Display the top element after pop
        stack.peek();
    }
}

# Python program to implement stack using Two Queue
from queue import Queue

class Stack:
    def __init__(self):
        self.q1 = Queue()
        self.q2 = Queue()

    # Push operation
    def push(self, value):
        self.q1.put(value)

    # Pop operation
    def pop(self):
        if self.is_empty():
            print("Stack is empty. Cannot pop.")
            return

        # Move elements from q1 to q2, except the last element
        while self.q1.qsize() > 1:
            self.q2.put(self.q1.get())

        # Pop the last element from q1
        self.q1.get()

        # Swap the names of q1 and q2
        self.q1, self.q2 = self.q2, self.q1

    # Check if the stack is empty
    def is_empty(self):
        return self.q1.qsize() == 0

    # Display the top element of the stack
    def peek(self):
        if self.is_empty():
            print("Stack is empty.")
            return

        # Move elements from q1 to q2, except the last element
        while self.q1.qsize() > 1:
            self.q2.put(self.q1.get())

        # Peek at the last element in q1
        print("Top element:", self.q1.queue[0])

        # Move the last element back to q1
        self.q2.put(self.q1.get())

        # Swap the names of q1 and q2
        self.q1, self.q2 = self.q2, self.q1

# Example usage of the stack
stack = Stack()

# Push elements onto the stack
stack.push(1)
stack.push(2)
stack.push(3)

# Display the top element
stack.peek()

# Pop an element
stack.pop()

# Display the top element after pop
stack.peek()

// C-Sharp program to implement stack using Queues
using System;
using System.Collections.Generic;

public class StackUsingQueue {
    class Stack {
        private Queue<int> q1 = new Queue<int>();
        private Queue<int> q2 = new Queue<int>();

        // Push operation
        public void Push(int value) {
            q1.Enqueue(value);
        }

        // Pop operation
        public void Pop() {
            if (IsEmpty()) {
                Console.WriteLine("Stack is empty. Cannot pop.");
                return;
            }

            // Move elements from q1 to q2, except the last element
            while (q1.Count > 1) {
                q2.Enqueue(q1.Dequeue());
            }

            // Pop the last element from q1
            q1.Dequeue();

            // Swap the names of q1 and q2
            Queue<int> temp = q1;
            q1 = q2;
            q2 = temp;
        }

        // Check if the stack is empty
        public bool IsEmpty() {
            return q1.Count == 0;
        }

        // Display the top element of the stack
        public void Peek() {
            if (IsEmpty()) {
                Console.WriteLine("Stack is empty.");
                return;
            }

            // Move elements from q1 to q2, except the last element
            while (q1.Count > 1) {
                q2.Enqueue(q1.Dequeue());
            }

            // Peek at the last element in q1
            Console.WriteLine("Top element: " + q1.Peek());

            // Move the last element back to q1
            q2.Enqueue(q1.Dequeue());

            // Swap the names of q1 and q2
            Queue<int> temp = q1;
            q1 = q2;
            q2 = temp;
        }
    }

    static void Main() {
        // Example usage of the stack
        Stack stack = new Stack();

        // Push elements onto the stack
        stack.Push(1);
        stack.Push(2);
        stack.Push(3);

        // Display the top element
        stack.Peek();

        // Pop an element
        stack.Pop();

        // Display the top element after pop
        stack.Peek();
    }
}

Output:

Top element: 3
Top element: 2

Time and Space Complexity.

In the above code, our pop operation is costly as we have to move all the remaining elements from Queue1 to Queue2. Similarly, we can implement the same approach by making push operation costly instead of pop operation.

Stack Operation	Time Complexity	Space Complexity
Push Operation	O(1)	O(1)
Pop Operation	O(N)	O(1)
IsEmpty	O(1)	O(1)

This approach cleverly utilizes two queues to represent stack behavior by employing element movements between the queues. While it successfully emulates a stack, it incurs some space overhead and may involve extra operations, such as queue swapping which could impact performance.

Stack Implementation using Single Queue.

In the above approach, we have used two queues to implement the stack operation. In this approach, we are going to use a single queue to implement the stack by manipulating the enqueue and dequeue operations to achieve the Last In, First Out (LIFO) behavior of the stack. 

Stack Operations:

Let's understand how we will implement two important stack operations push and pop using a single Queue:

Push Operation: To push an element onto the stack, enqueue the new element into the queue. To move the new element to the top, we have to rearrange elements in the queue by dequeuing elements before the newly added element and enqueuing them back to the queue.

Pop Operation: Popping is quite simple in this approach, we just have to dequeue and return the front element, which represents the topmost element of the stack.

Code for Stack Implementation Using Single Queue.

Below is the code implementation of the above approach:

C++ Java Python C#

// C++ program to implement stack using single Queue
#include<iostream>
#include<queue>
using namespace std;

class StackWithQueue {
private:
    queue<int> myQueue;
public:
    // function to push an element onto the stack
    void push(int value) {
        //get current size of queue
        int queueSize = myQueue.size();

        //enqueue a new element into queue
        myQueue.push(value);

        // rearrange the elements in the queue to 
        // make the new element the front (top)
        for(int i = 0; i < queueSize; i++) {
            myQueue.push(myQueue.front());
            myQueue.pop();
        }
    }
    // function to pop an element from the stack
    void pop() {
        if(myQueue.empty()) {
            cout << "Stack is Empty!"<<endl;
        }
        else {
            myQueue.pop();
        }      
    }
    // function to peek top element
    int peek() {
        if(myQueue.empty()){
            cout<< "Stack is Empty!"<<endl;
            return -1;
        }
        else {
            return myQueue.front();    
        }
    }
    // function to check if stack is empty
    bool isEmpty(){
        return myQueue.empty();
    }
    // function to get the size of stack
    int size() {
        return myQueue.size();
    }
};

//main function
int main() {
    StackWithQueue stack;

    stack.push(1);
    stack.push(2);
    stack.push(5);
    stack.push(8);
    
    cout<< stack.peek() <<endl;
    stack.pop();
    cout<< stack.peek() <<endl;

    return 0;
}

// Java Program to implement stack using Single Queue
import java.util.LinkedList;
import java.util.Queue;

public class StackWithQueue {
    private Queue<Integer> myQueue = new LinkedList<>();

    // Function to push an element onto the stack
    public void push(int value) {
        int queueSize = myQueue.size();
        myQueue.add(value);

        for (int i = 0; i < queueSize; i++) {
            myQueue.add(myQueue.poll());
        }
    }

    // Function to pop an element from the stack
    public void pop() {
        if (myQueue.isEmpty()) {
            System.out.println("Stack is Empty!");
        } else {
            myQueue.poll();
        }
    }

    // Function to peek top element
    public int peek() {
        if (myQueue.isEmpty()) {
            System.out.println("Stack is Empty!");
            return -1;
        } else {
            return myQueue.peek();
        }
    }

    // Function to check if the stack is empty
    public boolean isEmpty() {
        return myQueue.isEmpty();
    }

    // Function to get the size of the stack
    public int size() {
        return myQueue.size();
    }

    // Main function
    public static void main(String[] args) {
        StackWithQueue stack = new StackWithQueue();

        stack.push(1);
        stack.push(2);
        stack.push(5);
        stack.push(8);

        System.out.println(stack.peek());
        stack.pop();
        System.out.println(stack.peek());
    }
}

# Python code Implementation of stack using Single Queue
from queue import Queue

class StackWithQueue:
    def __init__(self):
        self.my_queue = Queue()

    # Function to push an element onto the stack
    def push(self, value):
        queue_size = self.my_queue.qsize()
        self.my_queue.put(value)

        for _ in range(queue_size):
            self.my_queue.put(self.my_queue.get())

    # Function to pop an element from the stack
    def pop(self):
        if self.my_queue.empty():
            print("Stack is Empty!")
        else:
            self.my_queue.get()

    # Function to peek top element
    def peek(self):
        if self.my_queue.empty():
            print("Stack is Empty!")
            return -1
        else:
            return self.my_queue.queue[0]

    # Function to check if the stack is empty
    def is_empty(self):
        return self.my_queue.empty()

    # Function to get the size of the stack
    def size(self):
        return self.my_queue.qsize()

# Main function
if __name__ == "__main__":
    stack = StackWithQueue()

    stack.push(1)
    stack.push(2)
    stack.push(5)
    stack.push(8)

    print(stack.peek())
    stack.pop()
    print(stack.peek())

// C# Program to implement stack using single Queue
using System;
using System.Collections.Generic;

public class StackWithQueue
{
    private Queue<int> myQueue = new Queue<int>();

    // Function to push an element onto the stack
    public void Push(int value)
    {
        int queueSize = myQueue.Count;
        myQueue.Enqueue(value);

        for (int i = 0; i < queueSize; i++)
        {
            myQueue.Enqueue(myQueue.Dequeue());
        }
    }

    // Function to pop an element from the stack
    public void Pop()
    {
        if (myQueue.Count == 0)
        {
            Console.WriteLine("Stack is Empty!");
        }
        else
        {
            myQueue.Dequeue();
        }
    }

    // Function to peek top element
    public int Peek()
    {
        if (myQueue.Count == 0)
        {
            Console.WriteLine("Stack is Empty!");
            return -1;
        }
        else
        {
            return myQueue.Peek();
        }
    }

    // Function to check if the stack is empty
    public bool IsEmpty()
    {
        return myQueue.Count == 0;
    }

    // Function to get the size of the stack
    public int Size()
    {
        return myQueue.Count;
    }

    // Main function
    public static void Main()
    {
        StackWithQueue stack = new StackWithQueue();

        stack.Push(1);
        stack.Push(2);
        stack.Push(5);
        stack.Push(8);

        Console.WriteLine(stack.Peek());
        stack.Pop();
        Console.WriteLine(stack.Peek());
    }
}

Output:

8
5

Time and Space Complexity.

Stack Operation	Time Complexity	Space Complexity
Push Operation	O(N)	O(1)
Pop Operation	O(1)	O(1)
IsEmpty	O(1)	O(1)

Stack Implementation Using Array.

Implementing a stack using an array involves using a fixed-size array to store elements and managing the stack operations by manipulating the array's indices. In this article, we will discuss stack implementation using an array and the advantages and disadvantages of using an array for this implementation.

Stack Implementation using Array.

An array provides a contiguous memory block to store stack elements, allowing direct access to elements via their indices. A top pointer or index is used to keep track of the top element of the stack within the array. 

Implementation of stack operations like push, pop, and peek is easy in array as we have direct access to elements using indices, providing constant-time access O(1). However, arrays have a fixed size, limiting the maximum capacity of the stack. 

Let's understand how to implement each stack operation using an array:

First of all, we have to define an array to store stack elements and initialize an index variable (top) to keep track of the top element.

Implement Push Operation:

• Create a push function that takes a value as input.
• Check if the stack is full (array size is reached), and handle overflow if needed.
• Increment the top pointer and insert the value at the incremented index.

Implement Pop Operation:

• Create a pop function.
• Check if the stack is empty (top is -1), and handle underflow if needed.
• Retrieve the value at the top index, decrement the top pointer, and return the value.

Implement Peek Operation:

• Create a peek function.
• Check if the stack is empty.
• Return the value at the top index without modifying the stack.

Implement isEmpty Operation:

• Create an isEmpty function.
• Check if the top pointer is -1 (indicating an empty stack).
• Return True if the stack is empty; otherwise, return False.

Stack Implementation Code.

Below is the code implementation of the stack using an array in C++, Java, Python, and C# language.

C++ Java Python C#

// C++ program to implement stack using array
#include <iostream>
using namespace std;

class Stack {
private:
    static const int MAX_SIZE = 1000; // Maximum size of the stack
    int arr[MAX_SIZE];
    int top;

public:
    Stack() : top(-1) {}

    // Push operation
    void push(int value) {
        if (top >= MAX_SIZE - 1) {
            cout << "Stack Overflow. Cannot push." << endl;
            return;
        }
        arr[++top] = value;
    }

    // Pop operation
    void pop() {
        if (isEmpty()) {
            cout << "Stack is empty. Cannot pop." << endl;
            return;
        }
        top--;
    }

    // Check if the stack is empty
    bool isEmpty() {
        return top == -1;
    }

    // Display the top element of the stack
    void peek() {
        if (isEmpty()) {
            cout << "Stack is empty." << endl;
            return;
        }
        cout << "Top element: " << arr[top] << endl;
    }
};

int main() {
    // Example usage of the stack
    Stack stack;

    // Push elements onto the stack
    stack.push(1);
    stack.push(2);
    stack.push(3);

    // Display the top element
    stack.peek();

    // Pop an element
    stack.pop();

    // Display the top element after pop
    stack.peek();

    return 0;
}

// Java program to implement stack using Array
public class Main {
  private static final int MAX_SIZE = 1000; // Maximum size of the stack

  static class Stack {
      private int[] arr;
      private int top;

      Stack() {
          arr = new int[MAX_SIZE];
          top = -1;
      }

      // Push operation
      void push(int value) {
          if (top >= MAX_SIZE - 1) {
              System.out.println("Stack Overflow. Cannot push.");
              return;
          }
          arr[++top] = value;
      }

      // Pop operation
      void pop() {
          if (isEmpty()) {
              System.out.println("Stack is empty. Cannot pop.");
              return;
          }
          top--;
      }

      // Check if the stack is empty
      boolean isEmpty() {
          return top == -1;
      }

      // Display the top element of the stack
      void peek() {
          if (isEmpty()) {
              System.out.println("Stack is empty.");
              return;
          }
          System.out.println("Top element: " + arr[top]);
      }
  }

  public static void main(String[] args) {
      // Example usage of the stack
      Stack stack = new Stack();

      // Push elements onto the stack
      stack.push(1);
      stack.push(2);
      stack.push(3);

      // Display the top element
      stack.peek();

      // Pop an element
      stack.pop();

      // Display the top element after pop
      stack.peek();
  }
}

# Python code to implement stack using array 
class Stack:
MAX_SIZE = 1000  # Maximum size of the stack

def __init__(self):
    self.arr = [0] * self.MAX_SIZE
    self.top = -1

# Push operation
def push(self, value):
    if self.top >= self.MAX_SIZE - 1:
        print("Stack Overflow. Cannot push.")
        return
    self.top += 1
    self.arr[self.top] = value

# Pop operation
def pop(self):
    if self.is_empty():
        print("Stack is empty. Cannot pop.")
        return
    self.top -= 1

# Check if the stack is empty
def is_empty(self):
    return self.top == -1

# Display the top element of the stack
def peek(self):
    if self.is_empty():
        print("Stack is empty.")
        return
    print("Top element:", self.arr[self.top])

# Example usage of the stack
stack = Stack()

# Push elements onto the stack
stack.push(1)
stack.push(2)
stack.push(3)

# Display the top element
stack.peek()

# Pop an element
stack.pop()

# Display the top element after pop
stack.peek()

// C-Sharp Code to implement stack using array
using System;

public class StackArray {
    private const int MAX_SIZE = 1000; // Maximum size of the stack

    class Stack {
        private int[] arr;
        private int top;

        public Stack() {
            arr = new int[MAX_SIZE];
            top = -1;
        }

        // Push operation
        public void Push(int value) {
            if (top >= MAX_SIZE - 1) {
                Console.WriteLine("Stack Overflow. Cannot push.");
                return;
            }
            arr[++top] = value;
        }

        // Pop operation
        public void Pop() {
            if (IsEmpty()) {
                Console.WriteLine("Stack is empty. Cannot pop.");
                return;
            }
            top--;
        }

        // Check if the stack is empty
        public bool IsEmpty() {
            return top == -1;
        }

        // Display the top element of the stack
        public void Peek() {
            if (IsEmpty()) {
                Console.WriteLine("Stack is empty.");
                return;
            }
            Console.WriteLine("Top element: " + arr[top]);
        }
    }

    static void Main() {
        // Example usage of the stack
        Stack stack = new Stack();

        // Push elements onto the stack
        stack.Push(1);
        stack.Push(2);
        stack.Push(3);

        // Display the top element
        stack.Peek();

        // Pop an element
        stack.Pop();

        // Display the top element after pop
        stack.Peek();
    }
}

Output:

Top element: 3
Top element: 2

Advantages of Array-based Stack.

• Implementing a stack using an array is straightforward and requires minimum code compared to linked list implementations.
• Array-based stacks offer efficient access to elements using indices, providing constant-time access O(1).
• Array uses contiguous memory, consuming less memory overhead compared to linked lists which require additional pointers for each node.

Disadvantages of Array-based Stack.

• Arrays have a fixed size, limiting the maximum capacity of the stack. This constraint requires predefined sizing or dynamic resizing logic to handle overflow conditions.
• Dynamic resizing to accommodate more elements involves creating a new array with increased capacity and copying existing elements, resulting in time complexity O(n) for resizing operations.
• If the array's size is significantly larger than the current number of stack elements, it can lead to memory wastage.

Related Post:

• Application of Stack Data Structure.
• Stack Implementation using LinkedList.

How To Delete Temporary Files in Windows.

Temporary files, accumulated during regular computer usage, can consume valuable disk space over time. Cleaning these files not only frees up storage but also contributes to smoother system performance. Here's a detailed step-by-step guide on how to efficiently delete temporary files in Windows, along with additional tips for optimizing your system.

How To Delete Temporary Files on Windows.

Deleting unnecessary temp files of your Windows system is an important task that you should perform at regular intervals. Let's learn how to delete temp files using Disk Cleanup on Windows.

Step 1: Press 'Windows key + S' to open the search box, type 'Disk Cleanup' and select the app from the search result.

Step 2: The Disk Cleanup utility will prompt you to select a drive. Choose the drive you want to clean (usually C:), and click 'OK.'

Step 3: The utility will calculate the space you can free up. In the Disk Cleanup dialog box, check the categories of files you want to delete, such as 'Temporary files' or 'Temporary Internet files.'

Quick Note: 'Temporary Files' refer to a broader category of temporary data created by applications and the operating system, while 'Temporary Internet Files' specifically pertain to temporary files generated by web browsers during internet browsing.

Step 4: Click 'OK' to confirm your selection, then click 'Delete Files' to initiate the cleanup process.

To access more cleanup options, click on 'Clean up system files' in the Disk Cleanup dialog. This allows you to remove system files, including the previous Windows installation if applicable.

How To Delete Temporary Files Using Command Prompt.

You can also delete your Windows temp files from the Command prompt using some basic simple commands. Let's learn how to do this:

Step 1: Press 'Windows + X' to open the Power User menu.

Step 2: Select 'Command Prompt (Admin)' or 'Windows PowerShell (Admin)' to open CMD with administrative privileges.

Step 3: In the Command Prompt window, type the following command and press Enter:

cd %temp%

Optionally, you can view the contents of the Temp folder by typing: dir

Step 4: To delete all files and subdirectories in the Temp folder, type:

del /s /q *

• /s includes files in all subdirectories.
• /q enables quiet mode, which doesn't prompt for confirmation.

Step 5: To navigate to the Prefetch folder, which contains additional temporary files, type:

cd C:\Windows\Prefetch

Step 6: To delete the contents of the Prefetch folder, type:

del /q *

Step 7: Type exit and press Enter to close the Command Prompt.

Don't forget to empty the Recycle Bin after deleting files to reclaim additional space.

Automate the Cleanup Process in Windows.

Deleting temp files using Disk Cleanup or Command Prompt is a manual process but you can also automate this process using Window's Settings. 

To schedule the cleanup process in Windows 11, Go to Settings > System > Storage > Configure Storage Sense or run it now. Enable Storage Sense to automatically free up space by deleting temporary files and you also change the default schedule time based on your need.

Another quick and easy method to automate this cleanup process is by creating a Batch File. 

Create a batch file containing the cleanup commands (shown below) and run it whenever needed. For example, create a text file with the extension .bat and include the commands:

cd %temp%
del /s /q *
cd C:\Windows\Prefetch
del /q *

For changes to take effect, consider restarting your computer after the cleanup.

Note: Be cautious when using the del command, especially with wildcard characters (*). Ensure you are in the intended directory before executing these commands to avoid unintentional data loss.

By following these steps and incorporating these tips, you can efficiently manage and delete temporary files on your Windows system, ensuring optimal performance and ample disk space. Regular cleanup is a proactive measure for maintaining a streamlined and responsive computing environment.