Check Balanced Parenthesis in an Expression.

Given an expression containing various types of parentheses ((), {}, []), you need to determine if the parentheses are balanced. An expression is considered balanced if every opening parenthesis has a corresponding closing parenthesis and they occur in the correct order.

Example:

Input: ({[]})

Output: true

Explanation: All pairs of parenthesis are balanced.

Input: ())(

Output: false

Explanation: All pairs of parenthesis are not balanced.

Input: [(){}]

Output: true

There are different ways to solve this problem and here we are going to discuss two of them:

Check Valid Balanced Parenthesis Using Stack.

In this approach, we use a stack data structure to solve this problem of checking balance parenthesis. It is because by nature parenthesis must occur in pairs and in the correct order and the stack LIFO property is best to handle such patterns.

Algorithm Steps to Validate Parenthesis:

Step 1: Initialize an empty stack to hold the opening parenthesis.

Step 2: Iterate through each character of the expression:

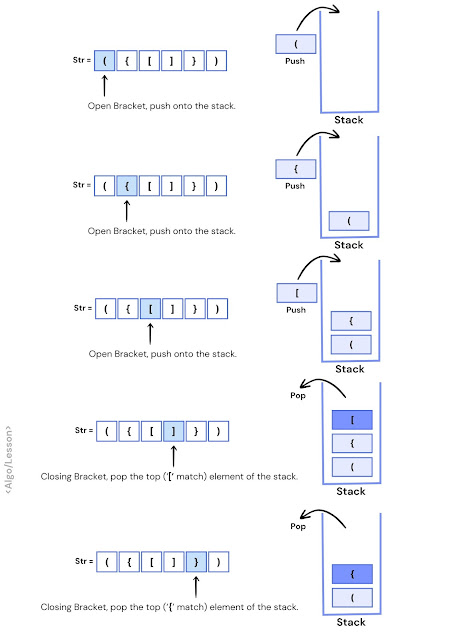
• If the character is an opening parenthesis ('(', '{', '['), push it onto the stack.
• If the character is a closing parenthesis (')', '}', ']') then check if the stack is empty then return false (unbalanced) else pop the top element and check if it matches with the closing parenthesis.
• If the closing parenthesis does not match with the top element of the stack then return false.

Step 3: After iteration, check if the stack is empty (balanced) and return true, else return false (unbalanced).

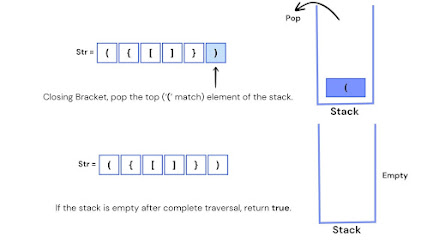
Example Illustration.

Below is the code implementation of the above approach:

C++ Java Python C#

// C++ code implementation to check balanced parenthesis
#include<iostream>
#include<stack>
using namespace std;

//function to check balance parenthesis
bool validParenthesis(string str){
    stack<char> st;

    for(int i = 0; i < str.size(); i++){
        //opening parenthesis, push into the stack
        if(str[i] == '{' || str[i] == '[' || str[i] == '(') {
            st.push(str[i]);    
        }else if(str[i] == '}' || str[i] == ']' || str[i] == ')') {
            
            //empty stack
            if(st.empty())
               return false;
            
            //check if stack top contain a matching opening bracket
            //pop the top element if matching is found
            if((st.top() == '{' && str[i] == '}') 
            || (st.top() == '[' && str[i] == ']') 
            || (st.top() == '(' && str[i] == ')')) {
                st.pop();
            }
            else{
                return false;
            } 
        }
    }
    //stack is empty after complete iteration
    if(st.empty()) 
       return true;
    
    return false;   
}
int main() {
    string str = "[{(){()}}]";

    if(validParenthesis(str)){
        cout<<"Balance Parenthesis"<<endl;
    }else{
        cout<<"Unbalance Parenthesis"<<endl;
    }
    return 0;
}

// Java Code Implementation to check balanced parenthesis
import java.util.Stack;

public class ParenthesisChecker {
    public static boolean isValidParenthesis(String str) {
        Stack<Character> stack = new Stack<>();
        //push the char in stack if they are opening brackets
        for (char ch : str.toCharArray()) {
            if (ch == '{' || ch == '[' || ch == '(') {
                stack.push(ch);
            } else if (ch == '}' || ch == ']' || ch == ')') {
                if (stack.isEmpty()) return false;
                
             
              //pop the top element if matching bracket is found
                char top = stack.pop();
                if ((top == '{' && ch == '}') || (top == '[' && ch == ']') 
                || (top == '(' && ch == ')')) {
                    continue;
                } else {
                    return false; // Mismatched brackets
                }
            }
        }

        return stack.isEmpty();
    }

    public static void main(String[] args) {
        String str = "[{(){()}}]";

        if (isValidParenthesis(str)) {
            System.out.println("Balanced Parenthesis");
        } else {
            System.out.println("Unbalanced Parenthesis");
        }
    }
}

# Python code to check balanced parenthesis
def is_valid_parenthesis(s):
stack = []

for char in s:
    # checking for open brackets
    if char in '{[(':
        stack.append(char)
    # checking for closing brackets    
    elif char in '})]':
        if not stack:
            return False
        
        # pop the top char from stack if matching pair is found
        top = stack.pop()
        if (top == '{' and char == '}') or (top == '[' and char == ']') or (top == '(' and char == ')'):
            pass
        else:
            return False  # Mismatched brackets

return not stack


# Example usage
parenthesis_str = "[{(){()}}]"
if is_valid_parenthesis(parenthesis_str):
print("Balanced Parenthesis")
else:
print("Unbalanced Parenthesis")

// C# code to check balanced parenthesis
using System;
using System.Collections.Generic;

class ParenthesisChecker
{
    static bool IsValidParenthesis(string str)
    {
        Stack<char> stack = new Stack<char>();

        foreach (char ch in str)
        {   // push the char in stack if it is opening bracket
            if (ch == '{' || ch == '[' || ch == '(')
            {
                stack.Push(ch);
            }
            // pop the top char from stack if it is matching pair of closing bracket 
            else if (ch == '}' || ch == ']' || ch == ')')
            {
                if (stack.Count == 0) return false;

                char top = stack.Pop();
                if ((top == '{' && ch == '}') || (top == '[' && ch == ']') 
                  || (top == '(' && ch == ')'))
                {
                    continue;// Matching brackets, continue
                }
                else
                {
                    return false; // Mismatched brackets
                }
            }
        }

        return stack.Count == 0;
    }

    static void Main()
    {
        string str = "[{(){()}}]";

        if (IsValidParenthesis(str))
        {
            Console.WriteLine("Balanced Parenthesis");
        }
        else
        {
            Console.WriteLine("Unbalanced Parenthesis");
        }
    }
}

Output:

Balanced Parenthesis

• Time Complexity: The algorithm iterates through each character in the expression once, resulting in a time complexity of O(n), where n is the length of the expression.
• Space Complexity: The space complexity is O(n), where n is the length of the expression. This is due to the stack storing opening parentheses, and in the worst case, the stack may contain all opening parentheses before encountering the corresponding closing ones.

Check Balanced Parenthesis Without Using Stack.

While the stack is a convenient data structure for checking balanced parentheses, it's possible to achieve the same goal without using a stack. 

Algorithm Steps:

Step 1: Initialize an integer variable i to -1. This variable will be used to track the top of the stack.

Step 2: Iterate through the expression:

• If ch is an opening parenthesis ('(', '{', '[') then increase the value of i by 1 and replace the character at index i in the expression with the opening bracket.
• If ch is a closing parenthesis (')', '}', ']') check if i is greater than or equal to 0. Check if the current closing bracket matches the corresponding opening bracket at index i: If yes, decrement i by 1 else returns false.

Step 3: After completing the iteration check if i is equal to -1 return true else return false.

Below is the code implementation of the above approach:

C++ Java Python C#

// C++ code to check balance parenthesis without stack
#include<iostream>
using namespace std;

//function to check parenthesis is balance or not
bool validParenthesis(string str) {
    // Initialize an index variable for tracking the top of the stack
    int i = -1;

    for(int j  = 0; j < str.size(); j++) {

        if(str[j] == '{' || str[j] == '[' || str[j] == '('){

           // Increment counter for opening parenthesis 
           i++;

           // Replace ith character with the opening bracket
           str[i] = str[j];
        }
        else{
          if(i >= 0 && ((str[i] == '(' && str[j] == ')') 
                     || (str[i] == '{' && str[j] == '}') 
                     || (str[i] == '[' && str[j] == ']'))) {
            // Decrement counter for matching closing parenthesis
            i--;
          }
          else {
            return false;
          }
        }
    }
    // -1 indicate that stack is empty (balanced parenthesis)
    if(i == -1) return true;
    
    return false;
}
int main() {
    string str = "({[][{]})";

    if(validParenthesis(str)){
        cout<<"Balance Parenthesis"<<endl;
    }else{
        cout<<"Unbalance Parenthesis"<<endl;
    }
    return 0;
}

// Java code implementation to check valid parenthesis
import java.util.Scanner;

public class Main {
    // Function to check if parentheses are balanced
    static boolean validParenthesis(String str) {
        StringBuilder sb = new StringBuilder();
        int i = -1;

        for (int j = 0; j < str.length(); j++) {
            char ch = str.charAt(j);

            if (ch == '{' || ch == '[' || ch == '(') {
                i++;
                sb.append(ch);
            } else {
                if (i >= 0 && ((sb.charAt(i) == '(' && ch == ')') || 

                   (sb.charAt(i) == '{' && ch == '}') || (sb.charAt(i) == '[' && ch == ']'))) {
                    i--;
                } else {
                    return false;
                }
            }
        }
        return i == -1;
    }

    public static void main(String[] args) {
        String str = "({[][{]})";

        if (validParenthesis(str)) {
            System.out.println("Balanced Parenthesis");
        } else {
            System.out.println("Unbalanced Parenthesis");
        }
    }
}

# Python program to validate parenthesis
def validParenthesis(s):
i = -1

for j in range(len(s)):
    if s[j] in ['{', '[', '(']:
        i += 1
        s = s[:i + 1] + s[j]
    else:
        if i >= 0 and ((s[i] == '(' and s[j] == ')') or (s[i] == '{' and s[j] == '}') or (s[i] == '[' and s[j] == ']')):
            i -= 1
        else:
            return False

return i == -1

str_value = "({[][{]})"
if validParenthesis(str_value):
print("Balanced Parenthesis")
else:
print("Unbalanced Parenthesis")

// C# code to check valid balanced parenthesis
using System;

class Program
{
    // Function to check if parentheses are balanced
    static bool ValidParenthesis(string str)
    {
        int i = -1;
        char[] sb = new char[str.Length];
        for (int j = 0; j < str.Length; j++)
        {
            char ch = str[j];

            if (ch == '{' || ch == '[' || ch == '(')
            {
                i++;
                sb[i] = ch;
            }
            else
            {
                if (i >= 0 && ((sb[i] == '(' && ch == ')') || (sb[i] == '{' && ch == '}') 

                   || (sb[i] == '[' && ch == ']')))
                {
                    i--;
                }
                else
                {
                    return false;
                }
            }
        }
        return i == -1;
    }

    static void Main()
    {
        string str = "({[][]})";

        if (ValidParenthesis(str))
        {
            Console.WriteLine("Balanced Parenthesis");
        }
        else
        {
            Console.WriteLine("Unbalanced Parenthesis");
        }
    }
}

Output:

Unbalanced Parenthesis

• Time Complexity: Time complexity of the above solution in O(n) where n is the length of the given expression.
• Space Complexity: Space complexity is O(1) if it is allowed to modify the existing string otherwise, it will be O(n).

Proper Nouns - Defination, Rules and Examples.

Welcome to the world of Proper Nouns! Have you ever wondered why some words get to wear capital letters like a crown? It is because, these are special words that give names to specific people, places, or things. In this article, we'll explore the magic of proper nouns and see how they make our language interesting and unique.

Definition of Proper Nouns.

A Proper noun is a type of noun that refers to a specific person, place, thing, or entity. They are always capitalized to distinguish them from common nouns. Unlike common nouns, which refer to general entities, proper nouns identify unique individuals or specific instances. Proper nouns can include names of people (e.g., John, Mary), places (e.g., New York City, Mount Everest), organizations (e.g., Google, NASA), and more.

Examples of Proper Nouns.

Some examples of proper nouns in sentences:

1. Person: Jessica invited her friend Alex to the birthday party.
2. Place: We went to Disneyland for our summer vacation.
3. Thing: I love drinking Coca-Cola with my meal.
4. Title: "The Lion King" is a popular animated film.
5. Organization: She works at Google as a software engineer.

Capitalization Rules of Proper Nouns.

Understanding how to capitalize proper nouns is like having a secret code to make names stand out in the world of words. Let's understand these rules with examples:

First Letter Capitalization.

• The first letter of each word in a proper noun should be capitalized. 
• Example: "New York City", where each word (New, York, City) starts with a capital letter.

Individual Names.

• When referring to people's names, both the first and last names should be capitalized. 
• Example: "Albert Einstein", where both "Albert" and "Einstein" are capitalized.

Titles.

• Titles that are part of a person's name, such as "Doctor", "Professor", or "Captain", should be capitalized.
• Example: "Captain Jack Sparrow" where "Captain" is part of the name and is capitalized.

Geographical Names.

• Names of specific places like counties, cities, mountains, rivers, and continents should have their first letter capitalized.
• Example: "The Great Wall of China" where all three words are capitalized.

Organizations.

• Names of companies, institutions, and organizations should begin with capital letters.
• Example: "Harvard University", where both "Harvard" and "University" are capitalized.

Brands and Products.

• Specific brand names, products, or trademarks are considered proper nouns and are capitalized.
• Example: "Nike Air Max" where "Nike", "Air" and "Max" are capitalized.

Days, Month, and Holidays.

• Names of days, months, and holidays are proper nouns and should be capitalized.
• Example: "July", "Friday", and "Christmas" are all capitalized.

Common Nouns Vs Proper Nouns.

Common nouns and Proper nouns both play an important role in our English language and Grammar. It is important to understand both and their differences so you can express your ideas clearly and accurately in written and spoken communication. 

Common nouns are the unspecific workhorses, representing general categories like 'girl', 'city', 'book', or 'happiness'. Their lowercase status, unless at the beginning of a sentence, allows them to seamlessly blend into everyday language. On the other hand, Proper nouns are the stars of specificity, offering individual names for particular people, places, or things. So, while common nouns populate our language with everyday elements, proper nouns add a touch of individuality, turning language into a rich tapestry of names and entities.

Possessive Forms of Proper Nouns.

The possessive forms of proper nouns involve indicating ownership or possession. To create a possessive form, add an apostrophe and an "s" ('s) to the end of the proper noun. When a proper noun owns something or is associated with possession, the 's is added to show possession. 

Example:

• Without Possessive Form: "John visited Mary"
• With Possessive Form: "John's car is parked outside"

In this example, "John" is a proper noun, and by adding 's, we create the possessive form "John's" indicating that the car belongs to John. This apostrophe-s construction is applied consistently to show ownership for various proper nouns.

FAQ on Proper Nouns.

Q1. Can common nouns become proper nouns?

Answer: Yes, common nouns can become proper nouns when they are used as specific names. For example, "river" (common noun) becomes "Nile River" (proper noun).

Q2. Can proper nouns be pluralized?

Answer: Yes, proper nouns can be pluralized by adding -s or -es, depending on the spelling. For example, "The Smiths" or "The Joneses."

Q3. What's a common mistake when using proper nouns?

Answer: A common mistake is failing to capitalize proper nouns. Always remember to start them with a capital letter.

Q4. Can a common noun and a proper noun coexist in a sentence?

Answer: Yes, a common noun and a proper noun can coexist, such as "The river (common noun) flows through Paris (proper noun)."

How To Remove an Image Background on Windows 11.

Removing the background from an image or replacing it with a different color can be essential for various purposes, such as creating professional-looking graphics or collages. While there are specialized tools for this task, you can achieve basic background removal on Windows 11 using built-in tools like Paint 3D or Photos app. 

Remove The Background of an Image.

You can use Windows built-in Paint application to delete or remove the entire background of an image and make it transparent. Here is a step-by-step guide to do that:

Step 1: First move to where you kept your image in File Explorer. Right-click on the image file you want to edit and select 'Open with' > 'Paint 3D.'

Step 2: After opening the image in Paint, in the 'Image' section at the top, select the 'Remove Background' option. 

Step 3: Wait for some time and you will see your edited image with a transparent background. 

Step 4: To save your image changes, click on File > Save As from the left Menu. Save your image as PNG to maintain the transparency as JPG does not support this format of the image.

Paint 3D allows you to undo and redo your actions. If you're not satisfied, use these options to go back and make adjustments.

If you do not want to remove the background of the entire image but only a selected part of the image then you can use the 'Selection' tool on the left top to select the specific portion of the image and then apply the 'Remove Background' option.

Change The Background Color of The Image.

If you don't want to make the background of the image transparent but want to change the background color, then you can do this as well on the Windows 11 Photo app without installing any additional tools. Let's learn how to do that:

Step 1: First move to where you kept your image in File Explorer. Right-click on the image file you want to edit and select "Open with" > "Photos."

Step 2: Once the image is loaded on the Photos app, click on 'Edit Image' on top.

Step 3: Click on the 'Background' option from the top toolbar. The Photos app will automatically detect the background of the image.

Step 4: You will get three options (Blur, Remove, and Replace) to modify your current image, choose 'Replace' and then select the color you want to fill in your image background. (see screenshot)

Step 5: When you are done with color selection, you can click on the 'Apply' button at the bottom right and then click on 'Save options' to save your edited image. That's it.

These are a few simple steps that you need to follow to change the background of any image on Windows 11 without downloading any additional third-party tool. 

How To Find WiFi Password in Windows 11.

Recently I bought a new laptop for my personal work and when I try to connect it from my home WiFi network I realize that I need to remember my WiFi password. For some time after struggling, I found some methods to find saved WiFi passwords from my previous Windows laptop. That day I also found that Windows stores all the WiFi passwords which has been used in the past to connect your device to the Internet. 

 

In this article, I am sharing two methods to find WiFi passwords on Windows and you can choose one based on your connivance.

Find WiFi Password on Windows Using Settings.

This is the simple and straightforward way to find WiFi passwords using Windows settings without using any third-party tool.

 

Step 1: Press "Windows key + I" to open Settings.

 

Step 2: Navigate to "Network & Internet" and select "WiFi" from the left pane. 

 

Step 3: Click on "Manage known networks."

 

Step 4: Choose your WiFi network, and under "Properties," you'll find the Network security key (password).

I hope you know where to go in your laptop to search all old WiFi passwords but make sure you have administrative privileges on the laptop and always double-check the network for security. Never connect your working or personal laptop to any unknown WiFi network. 

 

Find WiFi Password Using Command Prompt.

I am a tech-savvy person and I use Windows CMD and PowerShell a lot for many professional and personal work. I also find another method to fetch saved WiFi passwords from Windows CMD. Let's learn how to do that:

 

Step 1: Press "Windows key + X" on your keyboard. From the menu that appears, select "Command Prompt (Admin)" or "PowerShell (Admin)." This is crucial as administrative privileges are required for the following commands.

 

Step 2: Once the Command Prompt with administrative privileges is open, type the following command and press Enter. 

netsh wlan show profiles

This command will display a list of all WiFi profiles saved on your Windows laptop.

Step 3: Scroll through the list and identify your specific WiFi network name under the "User profiles" section.

Step 4: To reveal the password for a specific WiFi network, use the following command and press Enter. Replace "YOUR_NETWORK_NAME" with the actual name of your WiFi network (as identified in step 3).

netsh wlan show profile name="YOUR_NETWORK_NAME" key=clear

 

Step 5: This command will provide detailed information about the selected WiFi network, including the "Key Content," which is the WiFi password.

Both above methods to find WiFi passwords are efficient and simple. I personally choose CMD to fetch WiFi passwords because it gives me more insights into my network configurations.

How To Check Battery Health on Windows.

Ensuring the health of your Windows laptop's battery is crucial for prolonged usage and optimal performance as batteries play a pivotal role, in fueling our devices' vitality. However, batteries, much like the energy they provide, aren't eternal. This step-by-step guide provides insights into checking battery health and practical tips to enhance and maintain its longevity.

How To Check Windows Battery Health.

By running a simple line of code in Windows we can generate a complete health report of our battery in HTML file format. You can follow the below steps to generate the report:

Step 1: Press "Windows key + S," type "cmd," right-click on Command Prompt, and select "Run as administrator."

Step 2: In the Command Prompt, type the following command and press Enter. This command generates a battery report and saves it as an HTML file on your C: drive.

powercfg /batteryreport /output "C:\battery_report.html"

Step 3: Navigate to C:\ and locate the "battery_report.html" file. Open the file using a web browser to view detailed information about your battery's health.

The report provides insights into the battery's capacity, recent usage, and charging patterns.

Understanding Battery Health Report.

The Battery Report generated by your Windows laptop is akin to a comprehensive diary, chronicling the life and vitality of its power source. Let's dive into the key aspects it unfolds:

• Design Capacity: This represents the original capacity of your battery, essentially the amount it could store when it was brand new.

• Full Charge Capacity: The Full Charge Capacity showcases the current storage capacity of your battery. It's a real-time snapshot of how much energy your battery can currently hold.

• Cycle Count: The Cycle Count reveals the number of charge and discharge cycles your battery has undergone. A cycle is completed when your battery goes from 100% to 0% and back to 100%.

• Recent Usage: This section details your laptop's power consumption over the last several days, giving you insights into how your device utilizes its energy.

• Battery Drain Patterns: Examining the report unveils patterns of battery drain during different usage scenarios, shedding light on power-hungry applications or settings.

Understanding these metrics empowers you to make informed decisions about your laptop's energy source.

Tips to Improve Battery Health.

Taking care of your laptop battery health is in your own hands, you can follow some of our tips mentioned below to make your battery last longer.

• Try to avoid letting your battery drain completely before charging. Frequent deep discharges can contribute to wear and tear.
• Aim for partial discharge cycles (20-80%) rather than full 0-100% cycles. This can contribute to a longer battery lifespan.
• Adjust your power settings to balance performance and battery life. The "Power & sleep settings" in Windows allow you to choose power plans that suit your needs.
• Windows has a "Battery Saver" mode that conserves power by limiting background activity. Activate it when you need to extend battery life.
• Ensure your device drivers, especially those related to power management, are up to date. Check the manufacturer's website for the latest drivers.
• Lowering screen brightness can significantly impact battery life. Adjust brightness based on your environment to conserve power.

Conclusion.

By following these steps and implementing these tips, you can not only check the health of your Windows laptop's battery but also adopt practices that contribute to its longevity and sustained performance. Regular monitoring and mindful usage are key to ensuring your battery serves you well over time.

Difference Between == and .equals() in Java.

As a language, Java provides different mechanisms to compare objects and values. Two commonly used methods for comparison are the equals() method and the == operator. While they might seem similar, they serve different purposes and behave differently when used. Let's discuss each of them individually and understand which one should use in which condition.

== Operator.

In Java, the == operator is used to compare primitive data types and object references. When comparing primitive data types, it checks whether the values are the same. When comparing object references, it checks whether the references point to the same memory location.

Example Java Code:

public class EqualityExample {
    public static void main(String[] args) {
        // Primitive types
        int x = 5;
        int y = 5;
        System.out.println(x == y); // true

        // Object references
        String str1 = new String("Hello");
        String str2 = new String("Hello");
        System.out.println(str1 == str2); // false
    }
}

Output:

true
false

Explanation:

In the example, x == y is true because the values of x and y are both 5. However, str1 == str2 is false because the == operator compares the references, and str1 and str2 point to different memory locations.

equals() Methods.

The equals() method is a method provided by the Object class and is meant to be overridden by classes that need to define a logical equality. By default, the equals() method in the Object class compares object references, similar to the == operator.

Example Java Code:

public class EqualityExample {
    public static void main(String[] args) {
        String str1 = new String("Hello");
        String str2 = new String("Hello");
        System.out.println(str1.equals(str2)); // true
    }
}

Output:

true

Explanation:

In this example, str1.equals(str2) is true because the String class overrides the equals() method to compare the actual content of the strings, not just the references.

It's important to note that many classes in Java, like String, Integer, and others, override the equals() method to provide meaningful content-based comparison. When working with custom classes, you should override equals() to suit the specific equality criteria for instances of your class.

How To Schedule Cleanup Process in Windows.

Regularly scheduling cleanup processes in Windows is essential for maintaining optimal system performance and managing storage efficiently. This guide provides step-by-step instructions along with various methods to automate cleanup tasks, ensuring your system stays clutter-free.

Schedule Disk Cleanup with Task Scheduler.

Task Scheduler is a powerful built-in tool in Windows that allows you to automate various tasks, including cleanup processes. By creating scheduled tasks, you can ensure that cleanup routines occur regularly without manual intervention.

Step-by-step Guide:

Step 1: Press 'Windows key + S', type 'Task Scheduler', and select it from the search results.

Step 2: In the right-hand pane, click on 'Create Basic Task'.

Step 3: Provide a name and description for your task, then click 'Next'.

Step 4: Choose the trigger for your cleanup task (e.g., Daily, Weekly), and click 'Next'.

Step 5: Specify the start date and time for the task, and click 'Next'.

Step 6: Select 'Start a program'  as the action, and click 'Next'.

Step 7: In the "Program/script" field, enter the cleanup command (e.g., 'cleanmgr.exe' for Disk Cleanup). Add any arguments needed, like '/sagerun:1' for automated cleanup. Click 'Next'.

Step 8: Review your settings and click Finish.

Note: Test the task manually before relying on the scheduled run. You can set multiple triggers or conditions for more customized scheduling. 

How To Delete a Scheduled Task on Windows.

If you want to disable or delete the created scheduled task from Task Scheduler then you can follow these steps. 

Step-by-step Guide:

Step 1: Open Task Scheduler and in the left-hand pane, expand the 'Task Scheduler Library' to find the task.

Step 2: Right-click on the task you want to delete and select 'Delete' from the context menu.

Note: If you do not want to delete the task permanently then you can also disable them by selecting 'Disable' from the context menu.

Step 3: Confirm the deletion when prompted.

Deleting a task removes it permanently. Ensure you want to delete it before confirming. You can also check the task's status in the 'Active Tasks' tab before deleting or disabling the task.

Cleanup Process Using Storage Sense in Windows.

Storage Sense is a built-in feature in Windows 10 and 11 that automatically frees up space by deleting unnecessary files. This method is user-friendly and requires minimal configuration.

Step-by-step Guide:

Step 1: Press 'Windows key + I' to open Settings.

Step 2: Navigate to System > Storage.

Step 3: Click on 'Configure Storage Sense or run it now'.

Step 4: Toggle the switch to turn on Storage Sense. Choose the frequency and action for temporary file cleanup.

Step 5: Click on 'Advanced settings' to fine-tune cleanup options.

Storage Sense can automatically free up space by deleting temporary files, system-created files, and items in the recycle bin.

By following these methods, you can effortlessly schedule cleanup processes in Windows, ensuring your system remains optimized and clutter-free. Regular automated cleanup contributes to improved performance and efficient storage management.