The sliding Window Algorithm helps us solve many simple and complex coding problems with an optimized approach and lesser time complexity. In most cases, we use the sliding window algorithm to reduce the use of nested loops and the repetitive work that we do while solving any problem.
Why it is called Sliding Window Algorithm?
When we solve problems using this Sliding Window algorithm we try to create or find fixed-size or variable-size windows (here window is nothing but a subarray or substring) which satisfies the given condition of the problem and then we keep sliding the window by one unit to cover next subarrays.
We can easily find the required window (subarray) using two nested loops but the sliding window algorithm helps us find all possible windows by using a single loop and here now it helps us reduce our time complexity. The name of this algorithm is quite interesting and when we start visualizing the solution using this algorithm then everyone gets satisfied with the name of this algorithm.
When should we use Sliding Window Algorithm?
Whenever we want to use some algorithm to solve any particular problem we should always be trying to find some pattern in the given question like when we want to apply a binary search algorithm then we try to check whether the given array is sorted or not.
There are a few points that you can check for before using the sliding window algorithm:
- There should be some discussion related to subarray or substring in the given problem.
- There should be some discussion related to finding the largest, smallest, maximum, minimum, or any count.
- The problem might give us a window size denoting with variable k but if the window size is not given then it means we need to find the window size based on the given conditions.
Types of Sliding Windows.
We can solve several varieties of coding problems using the sliding window algorithm but more or less we can divide them into two different categories.
- Fixed Size Sliding Window: In this type, the size of the window (subarray) is static for the entire duration of the program and already given in the problem.
- Variable Size Sliding Window: In this type, the size of the window (subarray) is dynamic and keeps on changing for the entire duration of the program and we need to calculate the required largest or smallest window size.
Example of Fixed-size sliding window.
Given an array of integers of size n, find the minimum sum of the subarray of size k.
Example 1:
Input: arr[] = {2, 3, 5, 4, 9, 7, 1} k = 3
Output: 10
Explanation:
Sum of all possible subarrays of size 3
{2, 3, 5} = 2+3+5 = 10
{3, 5, 4} = 3+5+4 = 12
{5, 4, 9} = 5+4+9 = 18
{4, 9, 7} = 4+9+7 = 20
{9, 7, 1} = 9+7+1 = 17
The minimum sum we get by adding the subarray {2, 3, 5} of size 3.
Example 2:
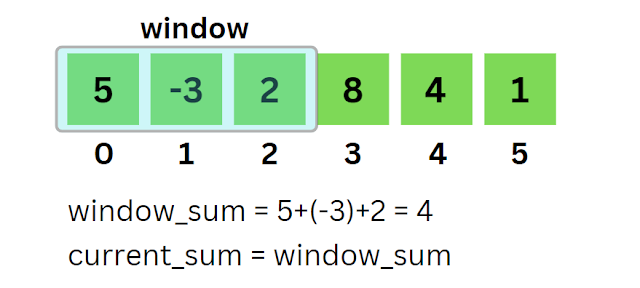
Input: arr[] = {5, -3, 2, 8, 4, 1} k = 2
Output: -1
Explanation:
The minimum sum we get by adding the subarray {-3, 2} of size 2
We can easily solve this problem using a brute force approach by running two nested loops for calculating the sum of all possible subarrays of size k and returning the minimum sum out of all possible. Time Complexity for this approach is O(n*k) where n is the number of elements and k is the size of the subarray.
Below is the code for the brute force approach:
//C++ Code for minimum sum of subarray of size k (O(n*k) solution) #include<iostream> using namespace std; int minSubarraySum(int arr[], int n, int k){ int minSum = INT_MAX; for(int i = 0; i < n-k; i++){ int sum = 0; for(int j = i; j < i+k; j++){ sum += arr[j]; } minSum = min(minSum, sum); } return minSum; } int main(){ int arr[] = {5, -3, 2, 8, 4, 1};
//size of given array int n = sizeof(arr)/sizeof(arr[0]); //size of subarray int k = 3; cout<<minSubarraySum(arr, n, k); }
Output:
4- Time Complexity: O(n*k)
- Space Complexity: O(1)
Now let's check that can we apply the sliding window algorithm to the above problem? As we discussed above for applying the sliding window algorithm, we can check for certain conditions like the problem is saying something about subarray, the window size k is given and we need to find the minimum subarray sum. It means the given problem satisfies all our conditions so we can think about applying the fixed-size sliding window approach here.
Sliding Window Algorithm: For applying the sliding window approach to this kind of problem where the window size is fixed we first need to compute the sum of the first k elements of the array and it will give us one possible answer that we can store in a variable window_sum. Now to slide the window by one unit to the right we need to remove the calculation of the first element of the previous window and add the last element of the current window.
We first calculate the initial window_sum starting from index 0 to 0+k and then we store it as a sum of our current window (current_sum) and we update our answer variable min_sum if current_sum is lesser than min_sum (initially min_sum = INT_MAX).- current_sum = 4
- min_sum = 4
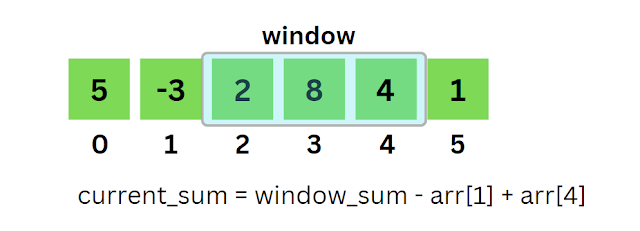
Now to get the sum of the next current_window we have to remove the first element from window_sum and add the last element of the current_window. Every time update the value of min_sum if the value of current_sum is smaller than min_sum.
- current_sum = 7
- min_sum = 4
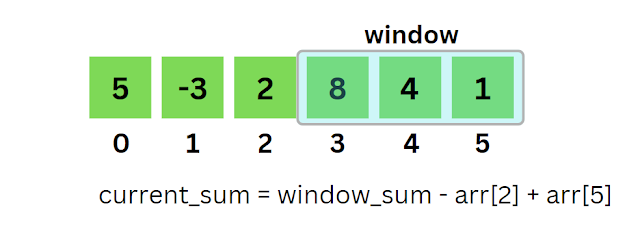
Similarly, again to get the sum of the next current_window we have to remove the first (arr[1]) element from window_sum and add the last element (arr[4]) of the current_window.
- current_sum = 14
- min_sum = 4
- current_sum = 13
- min_sum = 4
//C++ Code for minmum sum of subarray of size k (Sliding Window Approach)
#include<iostream> using namespace std; //function to find minmum sum of subarray of size k int minSubarraySum(int arr[], int n, int k){ //variable to store maxSum int minSum = INT_MAX; //variable to calculate window size int i = 0, j = 0; int window_sum = 0; while(j < n){ window_sum = window_sum + arr[j]; //Window size is less than k if(j-i+1 < k){ j++; } /*we get one of the possible answer, store it and remove the calculation of ith element and slide the window by one unit*/ else if(j-i+1 == k){ minSum = min(minSum, window_sum); window_sum = window_sum - arr[i]; i++; j++; } } return minSum; } int main(){ int arr[] = {5, -3, 2, 8, 4, 1}; //size of given array int n = sizeof(arr)/sizeof(arr[0]); //size of subarray int k = 3; cout<<minSubarraySum(arr, n, k); }
4- Time Complexity: O(n)
- Space Complexity: O(1)
After solving many fixed-size sliding window problems, I have observed a general pattern for this algorithm that you can also follow while solving problems.
Fixed-size Sliding Window General Format
while(j < n)
{
/*
In this step, we need to do calculation for
window formation base on given condition.
*/
if(current_window_size < k)
/*
Increase the window size as it is
not equal to given window size k
*/
j++;
else if(current_window_size == k)
{
/*
We get our one possible answer so store
them in some answer variable
*/
/*
Remove the calculation of ith index to
slide the window one unit right
*/
/*
Increment the vlaue of i and j to maintain
the window size
i++;
j++;
*/
}
}
return answer;
Example of Variable-size sliding window.
Example 1:
Input: arr[] = {8, 7, 3, 6, 1, 5} k = 15
Output: 4
Explanation:
The longest subarray with sum 15 is {3, 6, 1, 5}
Example 2:
Input: arr[] = {1, 2, 3} k = 3
Output: 2
Explanation:The longest subarray with sum 5 is {1, 2}
Input: arr[] = {-5, 7, -14, 3, 4, 12} k = -5Output: 5Brute Force: We find the sum of all possible subarrays and return the length of the longest subarray having a sum equal to k. The time complexity of this approach is O(n^2) as we are calculating the sum of all subarrays.
Below is the C++ Code Implementation.
#include<iostream> using namespace std; //function to find longest subarray of sum k int longestSubarraySum(int arr[], int n, int k){ //variable to store answer int maxlen = 0; for(int i = 0; i < n; i++){ int sum = 0; for(int j = i; j < n; j++){ sum += arr[j]; if(sum == k){ maxlen = max(maxlen, j-i+1); } } } return maxlen; } int main(){ int arr[] = {10, 5, 2, 7, 1, 9}; //given array size int n = sizeof(arr)/sizeof(arr[0]); int k = 15; cout<<longestSubarraySum(arr, n, k); }
4- Time Complexity: O(n^2)
- Space Complexity: O(1)
- When the sum is less than k, we need to add more variables and increment j.
- When the sum is equal to k, we get one possible answer and store the length of the current subarray in some max variable.
- When the sum is greater than k, then subtract the ith elements until the sum becomes less than k.
#include<iostream> using namespace std; //function to find longest subarray of sum k (Sliding Window approach) int longestSubarraySum(int arr[], int n, int k){ //variable to store answer int i = 0, j = 0, sum = 0; int maxlen = INT_MIN; while(j < n){ sum += arr[j]; //sum is less than k if(sum < k){ j++; } //sum is equal to k else if(sum == k){ maxlen = max(maxlen, j-i+1); j++; } //sum is greater than k else if(sum > k){ //remove ith elements until sum //again become equal or less than k while(sum > k){ sum -= arr[i]; i++; } if(sum == k){ maxlen = max(maxlen, j-i+1); } j++; } } return maxlen; } int main(){ int arr[] = {10, 5, 2, 7, 1, 9}; //given array size int n = sizeof(arr)/sizeof(arr[0]); int k = 15; cout<<longestSubarraySum(arr, n, k); }
4- Time Complexity: O(n)
- Space Complexity: O(1)
After solving many variable-size sliding window problems, I have observed a general pattern for this algorithm that you can also follow while solving problems.
Variable-size Sliding Window General Format
while(j < n)
{
/*
we need to do [calculation] for window
formation base on given condition.
*/
if(calculation < k)
{
/*
Increase the window size as calculation
is not matching with given condition k
*/
j++;
}
else if(calculation == k)
{
/*
we get our one possible answer, store them in some variable
Increment the value of j.
*/
}
else if(calculation > k)
{
/*
start removing ith elements to from calculation
so it again meet our condition calculation == k
*/
while(condition > k)
{
//remove calculation for i
i++;
}
//check if we are meeting the given condition
j++;
}
}
return answer;







.png)







